2025年成考高起点每日一练《数学(理)》5月27日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、从1、2、3、4、5、6、7、8、9这九个数字中,随机取出一个数字,这个数字是奇数的概率是()。
- A:
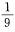
- B:
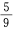
- C:
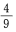
- D:
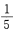
答 案:B
解 析:本题的试验是从1~9这九个数字中任取一个数字,显然选中其中任一个数字的可能 性都是相同的,属于等可能事件的概率,∵n=9,其中奇数个数m=5,∴其概率是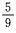 ,故选B。
,故选B。
2、设f(x)=ax+b目f(0)=-2,f(3)=4,则f(2)=()。
- A:6
- B:2
- C:1
- D:0
答 案:B
3、参数方程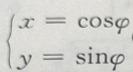 (
( 为参数)表示的图形为()
为参数)表示的图形为()
- A:直线
- B:圆
- C:椭圆
- D:双曲线
答 案:B
解 析: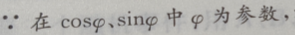
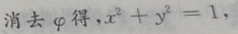 即半径为1的圆,圆心在原点
即半径为1的圆,圆心在原点
4、命题甲:实数a,b,c成等比数列;命题乙:b2=ac,则甲是乙()。
- A:充分条件但不是必要条件
- B:必要条件但不是充分条件
- C:充分必要条件
- D:不是充分条件也不是必要条件
答 案:A
主观题
1、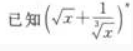 展开式的二项式系数之和比
展开式的二项式系数之和比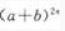 展开式的二项式系数之和小240。 求:(1)
展开式的二项式系数之和小240。 求:(1)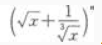 展开式的第3项;
展开式的第3项;
(2)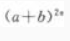 展开式的中间项。
展开式的中间项。
答 案:
2、设函数f(x)=xlnx+x.(I)求曲线y=f(x)在点((1,f(1))处的切线方程;
(II)求f(x)的极值.
答 案:(I)f(1)=1,f'(x)=2+lnx,故f'(1)=2.所以曲线y=f(x)在点(1,f(1))处的切线方程为y=2x-1.(II)令f'(x)=0,解得 当
当 时,f'(x)
时,f'(x) 单调递减,在区间
单调递减,在区间 单调递增.因此f(x)在
单调递增.因此f(x)在 时取得极小值
时取得极小值
3、设函数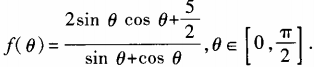 (1)求
(1)求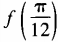 ;(2)求函数f(θ)最小值。
;(2)求函数f(θ)最小值。
答 案:
4、设 (0<α<π),求tanα的值。
(0<α<π),求tanα的值。
答 案:
填空题
1、函数 的定义域是()
的定义域是()
答 案: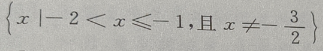
解 析: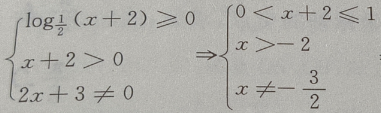
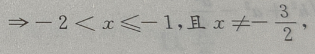 所以函数
所以函数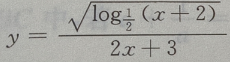 的定义域是
的定义域是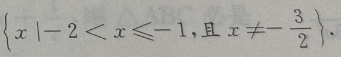
2、函数y=2cosx-cos2x(x∈R)的最大值为______。
答 案: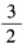
解 析: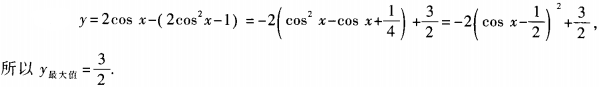
精彩评论