2025年成考专升本每日一练《高等数学二》5月12日专为备考2025年高等数学二考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析:
单选题
1、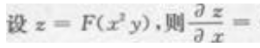 ()。
()。
- A:
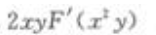
- B:
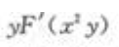
- C:
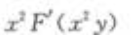
- D:
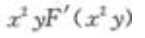
答 案:A
解 析:
2、下列命题正确的是().
- A:函数f(x)的导数不存在的点,一定不是f(x)的极值点
- B:若x0为函数f(x)的驻点,则x0必为f(x)的极值点
- C:若函数f(x)在点x0处有极值,且f'(x0)存在,则必有f'(x0)=0
- D:若函数f(x)在点x0处连续,则f'(x0)一定存在
答 案:C
解 析:AD两项,设f(x)=|x|,显然x=0是函数的极小值点,且函数在该点也连续,但函数在该点不可导;B项,设f(x)=x3,显然x0=0是函数的驻点,但x0=0不是函数的极值点;C项,根据函数在点x0处取极值的必要条件的定理,可知选项C是正确的.
主观题
1、证明:当x>1时,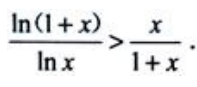
答 案:证:设F(x)=(1+x)ln(1+x)-xlnx.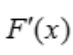 =ln(1+x)+1-lnx-1
=ln(1+x)+1-lnx-1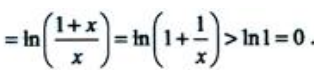 所以,当x>1时,
所以,当x>1时,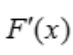 >0,即F(x)单调增加.
>0,即F(x)单调增加.
当x>1时,F(x)>F(1)=2ln2>0,即(1+x)ln(1+x)-xlnx>0.所以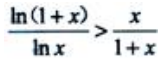 .
.
2、设随机变量ξ的分布列为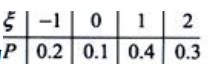 求E(ξ)和D(ξ).
求E(ξ)和D(ξ).
答 案:解:E(ξ)=-1×0.2+0×0.1+1×0.4+2×0.3=0.8.D(ξ)=(-1-0.8)2×0.2+(0-0.8)2×0.1+(1-0.8)2×0.4+(2-0.8)×0.3=1.16.
填空题
1、若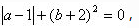 则
则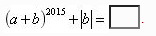
答 案:1
2、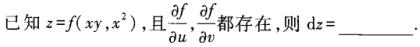
答 案: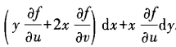
解 析:本题考查的知识点是复合函数求偏导和全微分的计算公式。 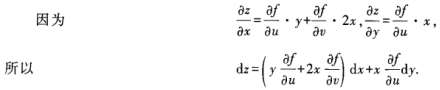
简答题
1、已知函数f(x)=ax3-bx2+cx在区间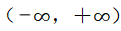 内是奇函数,且当x=1时,f(x)有极小值
内是奇函数,且当x=1时,f(x)有极小值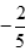 ,求另一个极值及此曲线的拐点.
,求另一个极值及此曲线的拐点.
答 案:f(x)=ax3-bx2+cx,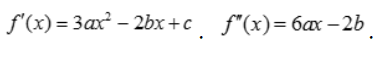 由于f(x)是奇函数,则必有x2的系数为0,即b=0.
由于f(x)是奇函数,则必有x2的系数为0,即b=0.
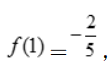 即a+c=
即a+c=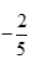 ,
,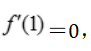 得3a+c=0.解得a=
得3a+c=0.解得a=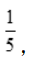 c=
c= 此时
此时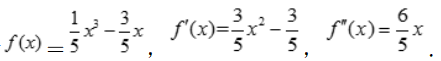 令
令 得
得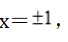
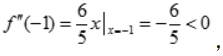 所以
所以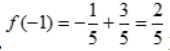 为极大值,
为极大值,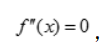 得x=0,x<0时,
得x=0,x<0时,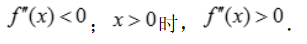 所以(0,0)为曲线的拐点.
所以(0,0)为曲线的拐点.
2、设z=z(x,y)是由方程x2+y2+z2=ez所确定的隐函数,求dz。
答 案:
精彩评论