2025年成考专升本每日一练《高等数学一》5月2日专为备考2025年高等数学一考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、设函数 ,则f(x)的导数f'(x)=()。
,则f(x)的导数f'(x)=()。
- A:

- B:

- C:

- D:
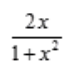
答 案:C
解 析:由可变限积分求导公式 可知
可知
2、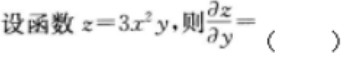
- A:6Y
- B:6XY
- C:3X
- D:3X2
答 案:D
3、极限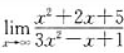 等于()。
等于()。
- A:5
- B:

- C:3
- D:0
答 案:B
解 析: 。
。
主观题
1、某厂要生产容积为V0的圆柱形罐头盒,问怎样设计才能使所用材料最省?
答 案:解:设圆柱形罐头盒的底圆半径为r,高为h,表面积为S,则 由②得
由②得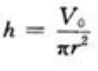 ,代入①得
,代入①得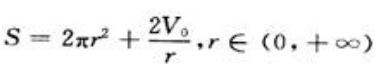
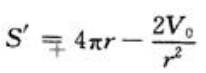 现在的问题归结为求r在(0,+∞)上取何值时,函数S在其上的值最小。
现在的问题归结为求r在(0,+∞)上取何值时,函数S在其上的值最小。
令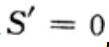 ,得
,得
由②,当 时,相应的h为:
时,相应的h为: 。
。
可见当所做罐头盒的高与底圆直径相等时,所用材料最省。
2、求微分方程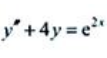 的通解。
的通解。
答 案:解: 的特征方程为
的特征方程为 ,则特征根为
,则特征根为 ,故其通解为
,故其通解为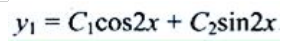 因为自由项
因为自由项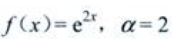 不是特征根,故设特殊解为
不是特征根,故设特殊解为 代入原方程,有
代入原方程,有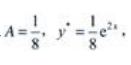 故
故 的通解为
的通解为
3、求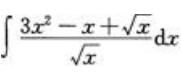 。
。
答 案:解:
填空题
1、过点(1,0,-1)与平面3x-y-z-2=0平行的平面的方程为()
答 案:3x-y-z-4=0
解 析:平面3x-y-z-2=0的法向量为(3,-1,-1),所求平面与其平行,故所求的平面的法向量为(3,-1,-1),由平面的点法式方程得所求平面方程为3(x-1)-(y-0)-(z+1)=0,及3x-y-z-4=0。
2、微分方程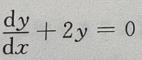 的通解为y=()
的通解为y=()
答 案: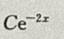
解 析:将微分方程变量分离,可得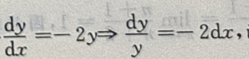 两边同时积分
两边同时积分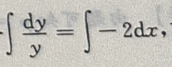 可得In|y|
可得In|y|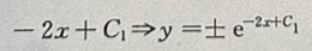
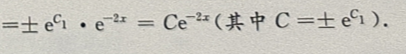
3、设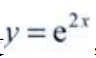 ,则
,则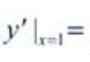 ()。
()。
答 案:2e2
解 析: ,则
,则
简答题
1、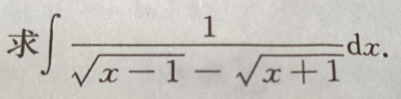
答 案:
精彩评论