2025年成考专升本每日一练《高等数学一》4月27日专为备考2025年高等数学一考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、对于微分方程y"+2y'+y=ex,利用待定系数法求其特解y*时,其形式可以设为()。
- A:y*=Axex
- B:y*=Aex
- C:y*=(Ax+B)ex
- D:y*=ex
答 案:B
解 析:该微分方程的特征方程为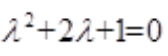 ,解得
,解得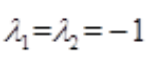 ,故特解形式可以设为y*=Aex。
,故特解形式可以设为y*=Aex。
2、在空间直角坐标系中,方程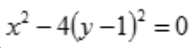 表示()。
表示()。
- A:两个平面
- B:双曲柱面
- C:椭圆柱面
- D:圆柱面
答 案:A
解 析:由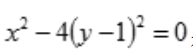 得
得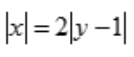 ,故为两个平面。
,故为两个平面。
3、幂级数 的收敛半径是()。
的收敛半径是()。
- A:1
- B:3
- C:13
- D:∞
答 案:B
解 析: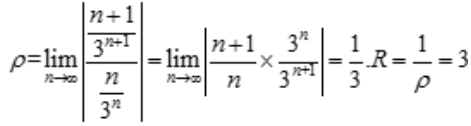 。
。
主观题
1、判定级数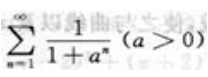 的敛散性.
的敛散性.
答 案:解: 含有参数a>0,要分情况讨论:(1)如果0<a<1,则
含有参数a>0,要分情况讨论:(1)如果0<a<1,则 ,由级数收敛的必要条件可知,原级数发散。(2)如果a>1,令
,由级数收敛的必要条件可知,原级数发散。(2)如果a>1,令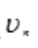 =
=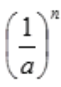 ;因为
;因为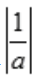 <1,因而
<1,因而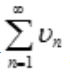 是收敛的,比较法:
是收敛的,比较法: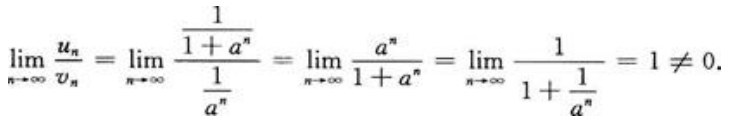
所以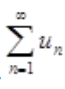 也收敛。
也收敛。
(3)如果a=1,则 所以
所以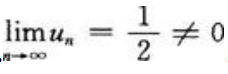 ,由级数收敛的必要条件可知,原级数发散。所以
,由级数收敛的必要条件可知,原级数发散。所以
2、计算
答 案:解:令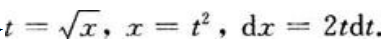 当x=4时,t=2;当x=9时,t=3。则有
当x=4时,t=2;当x=9时,t=3。则有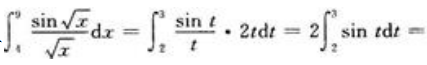
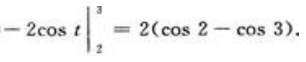
3、求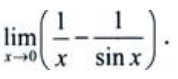
答 案:解: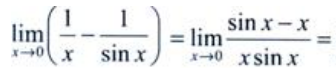
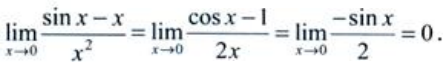
填空题
1、曲线y=x2-x在点(1,0)处的切线斜率为()。
答 案:1
解 析:点(1,0)在曲线y=x2-x上,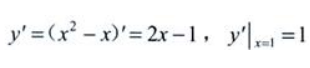 ,故点(1,0)处切线的斜率为1。
,故点(1,0)处切线的斜率为1。
2、设区域D由y轴,y=x,y=1所围成,则
答 案: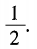
解 析:本题考查的知识点为计算二重积分。其积分区域如图1-1阴影区域所示: 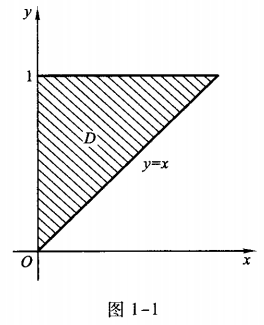
可利用二重积分的几何意义或将二重积分化为二次积分解之。
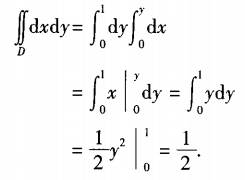
3、已知函数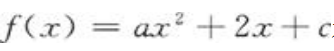 在点x=1处取得极值2,则a=(),c=(),1为极()值点。
在点x=1处取得极值2,则a=(),c=(),1为极()值点。
答 案:-1,1,大
解 析: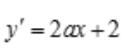 ,
,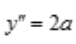 ,由于(1,2)在曲线y=ax2+2x+c上,又x=1为极值点,所以y'(1)=0,有
,由于(1,2)在曲线y=ax2+2x+c上,又x=1为极值点,所以y'(1)=0,有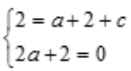 解得a=-1,c=1,
解得a=-1,c=1,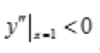 ,则x=1为极大值点。
,则x=1为极大值点。
简答题
1、求函数f(x)=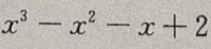 的单调区间。
的单调区间。
答 案: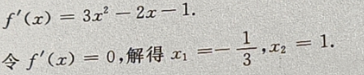
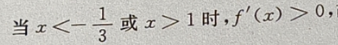
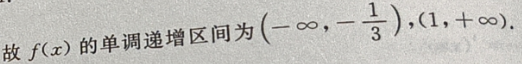


精彩评论