2025年成考高起点每日一练《数学(理)》4月26日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、已知 ,则sin2α=()
,则sin2α=()
- A:
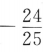
- B:
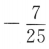
- C:
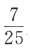
- D:
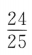
答 案:D
解 析: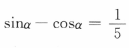 两边平方得
两边平方得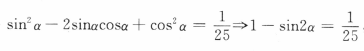 ,故
,故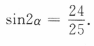
2、若函数f(x)是奇函数,则函数 的奇偶性是()。
的奇偶性是()。
- A:奇函数
- B:偶函数
- C:非奇非偶函数
- D:即是奇函数,又是偶函数
答 案:A
解 析:∵f(x)是奇函数
∴f(-x)=-f(x)
∵F(x)=f(x)·(-cosx)=-f(x)cosx
∴F(-x)=-f(-x)cos(-x)= f(x)cosx =-F(x)
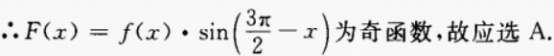 注:由此可知,奇函数×偶函数为奇函数;奇函数×奇函数为偶函数;偶函数×偶函数为偶函数。
注:由此可知,奇函数×偶函数为奇函数;奇函数×奇函数为偶函数;偶函数×偶函数为偶函数。
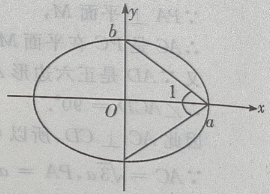
3、从椭圆与x轴额右交点看短轴两端点的视角为60°的椭圆的离心率()
- A:
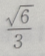
- B:
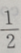
- C:1
- D:
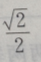
答 案:A
解 析:求椭圆的离心率,先求出a,c.(如图) 
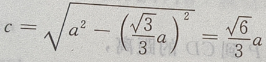 ,由椭圆定义知
,由椭圆定义知
4、已知球的大圆周长是π,则这个球的表面积是()。
- A:
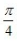
- B:4π
- C:2π
- D:π
答 案:D
主观题
1、求将抛物线y=x2-2x-3平移到顶点与坐标原点重合时的函数解析式。
答 案:
2、设函数f(x)= (Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值
(Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值
答 案:(Ⅰ)函数的定义域为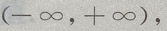
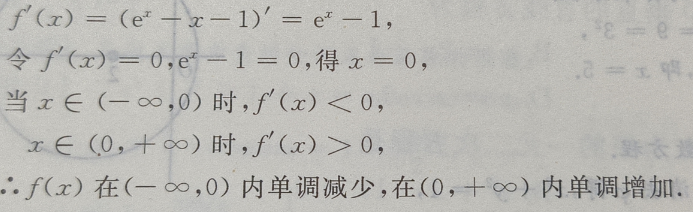 (Ⅱ)
(Ⅱ)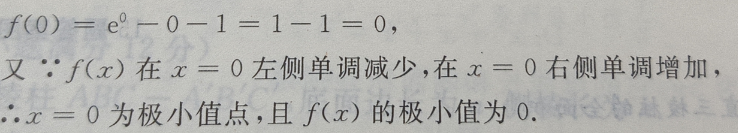
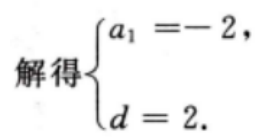
3、已知等差数列{an}中,a1+a2+a3=6,a2+a4+a5= 12求{an}的首项与公差。
答 案:因为{an}为等差数列,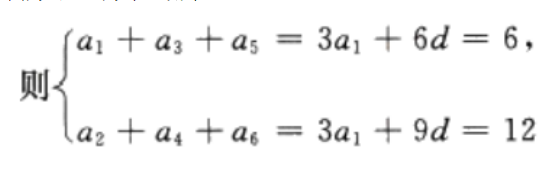
4、已知am=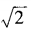 ,an=
,an=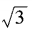 ,求a3n-4m的值。
,求a3n-4m的值。
答 案: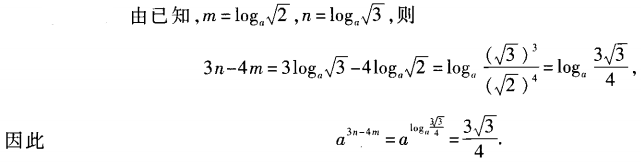
填空题
1、若tanα-cotα=1,则 =______。
=______。
答 案:4
解 析:由立方差公式得,tan3α-cot3α=(tana-cotα)(tan2α+tanαcota+cot2α)(tana-cotα)[(tanα-cotα)2+3tanαcotα]=4
2、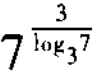 =______。
=______。
答 案:27
解 析: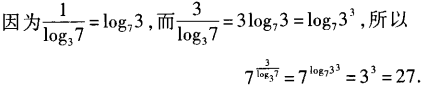
精彩评论