2025年成考高起点每日一练《数学(文史)》4月21日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、通过点(-3，1)且与直线3x-y-3=0垂直的直线方程是（　）

• A：x+3y=0
• B：3x+y=0
• C：x-3y+6=0
• D：3x-y-6=0

答 案：A

解 析：直线3x-y-3=0的斜率k=3，因为所求直线与已知直线垂直，所以所求直线的斜率k1=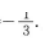 又所求直线过点(-3,1),所以所求直线的方程为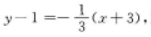即是x+3y=0.

2、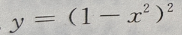的导数是  

• A：
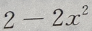
• B：
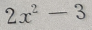
• C：
• D：

答 案：C

解 析：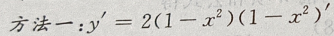

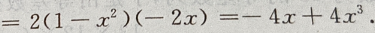
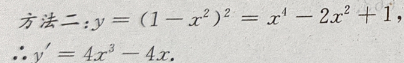
3、y=(2x²+3)(3x-2)的导数是（　）

• A：18x²-8x+9
• B：6x²+9
• C：12x²-8x
• D：12x

答 案：A

解 析：y=(2x²+3)(3x-2)=6x³-4x2+9x-6，y´=18x²-8x+9．【考点指要】会用两个函数和、差的求导法则求多项式函数的导数，是近几年成人高考的常见题．

4、已知a，b为任意正实数，则下列等式中恒成立的是（）。

• A：a^b=b^a
• B：2^a+b=2^a+2^b
• C：
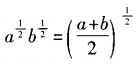
• D：a^lgb=b^lga

答 案：D

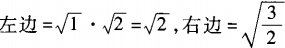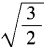解 析：由于a，b为任意正实数，不妨取a=1，b=2。在A项中，1²≠2¹；B项中，2¹⁺²≠2¹+2²；C项中，，而≠。故选D。

主观题

1、在△ABC中,已知三边 a、b、c 成等差数列,且最大角∠A是最小角的2倍, a: b :c.  

答 案：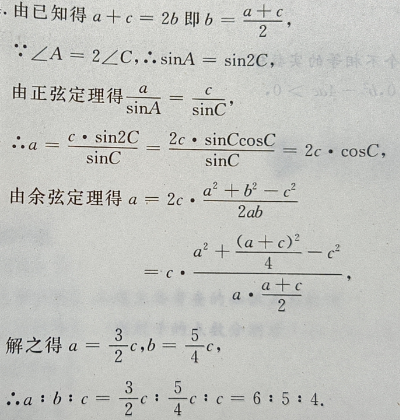

2、已知tan²θ=2tan²ψ+1，求cos2θ+sin²ψ的值。  

答 案：由已知，得

3、如图9-4，已知测速站P到公路L的距离为40米，一辆汽车在公路L上行驶，测得此车从A点行驶到8点所用的时间为2秒，并测得∠APO=60°，∠BPO=30°，计算此车从A到B的平均速度为多少km/h（结果保留到个位），并判断此车是否超过了80km/h的限制速度。

答 案：此车从A到B的平均速度为83（km/h），已经超过80km/h的限制速度。

4、已知lg2=a，lg3=b，求lg0.15关于a，b的表达式。  

答 案：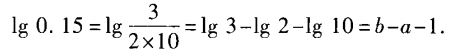

填空题

1、从某班的一次数学测试卷中任意抽出10份,其得分情况如下:81,98,43,75,60,55,78,84,90,70,则这次测验成绩的样本方差是（）  

答 案：252.84

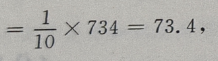
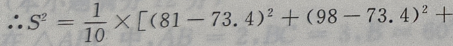
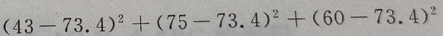
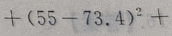
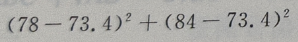
解 析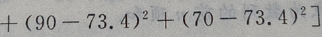： =252.84  

2、已知tanθ=1/2，则sin2θ+sin2θ=__________．

答 案：1

解 析：