2025年成考高起点每日一练《数学(理)》4月17日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、在△ABC中,∠C=90°,∠B=30°,D是BC上的一点,∠ADB=135°,AC=2,则BD等于()。
- A:
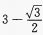
- B:
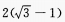
- C:
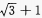
- D:
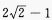
答 案:B
解 析:由已知得,AC=CD=2,设BD=x,在Rt△ABC中,BC=2cot30°=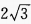
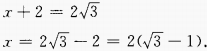
2、函数y=x2—2x+6在区间(-∞,1)、(1,+∞)分别()。
- A:单调增加、单调减少
- B:单调减少、单调增加
- C:单调增加、单调增加
- D:单调减少、单调减少
答 案:B
解 析:方法一:用配方法把y=x2-2x+6配成完全平方式。 y=x2-2x+6=(x-1)2+5,开口向上的抛物线顶点坐标为(1,5),可得出单调区间。 方法二:用导数判定。y’=2x-2=2(x-1)
当x<1时,y’<0,单调减少;当x>1时,y>0,单调增加。
3、抛物线y2=2px上任意一点与焦点连线中点的轨迹方程是()。
- A:
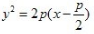
- B:
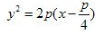
- C:

- D:
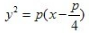
答 案:D
4、已知球的大圆周长是π,则这个球的表面积是()。
- A:
- B:4π
- C:2π
- D:π
答 案:D
主观题
1、设函数f(x)= (Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值
(Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值
答 案:(Ⅰ)函数的定义域为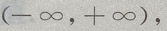
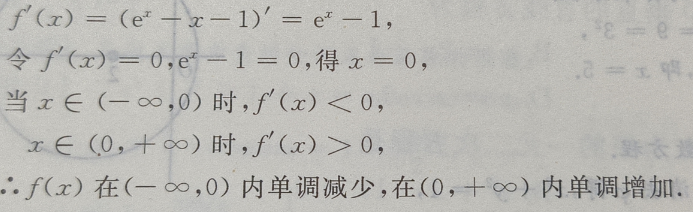 (Ⅱ)
(Ⅱ)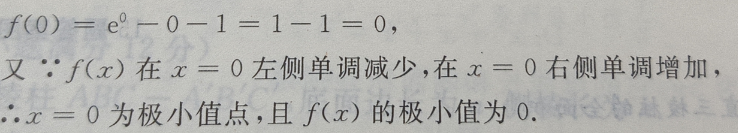
2、在△ABC中如果sinA=2sinBcosC,求证:△ABC是等腰三角形。
答 案: ∴△ABC为等腰三角形。
∴△ABC为等腰三角形。
3、求下列函数的定义域: (1)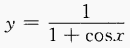
(2)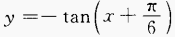
(3)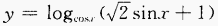
答 案:(1) 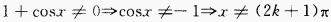 ∴函数的定义域为
∴函数的定义域为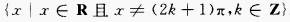 (2)
(2) 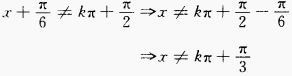 ∴函数的定义域为
∴函数的定义域为 (3)
(3)
由对数函数的性质知,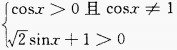
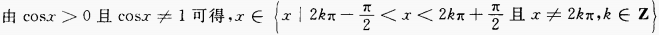
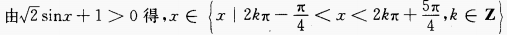 故函数的定义域为
故函数的定义域为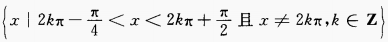
4、已知抛物线C:y2=2px(p>0)的焦点到准线的距离为1。 (I)求C的方程; (Ⅱ)若A(1,m)(m>0)为C上一点,O为坐标原点,求C上另一点B的坐标,使得OA⊥OB
答 案:(I)由题意,该抛物线的焦点到准线的距离为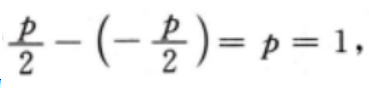 所以抛物线C的方程为
所以抛物线C的方程为 (Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得
(Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得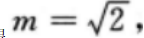 因此A点坐标为
因此A点坐标为 设B点坐标为
设B点坐标为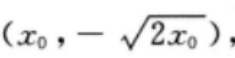 则
则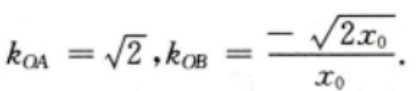 因为
因为 则有
则有 即
即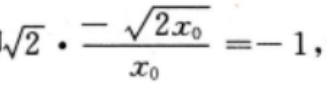 解得x0=4
所以B点的坐标为
解得x0=4
所以B点的坐标为
填空题
1、不等式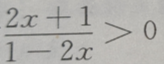 的解集为()
的解集为()
答 案: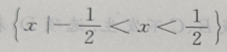
解 析:

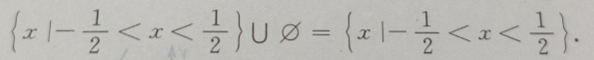
2、已知函数y=a2+bx+c的图像是以(6,-12)为顶点的抛物线,并且与x轴的一个交点坐标是(8,0),则a=(),b=(),c=()
答 案: 3;-36;96
解 析:根据顶点坐标是(6,-12),设y=a(x-6)2-12(8,0)代入得:0=a*(8-6)2-12得到a=3
即y=3(x-6)2-12=3x2-36x+96
故a=3,b=-36,c=96
精彩评论