2025年成考专升本每日一练《高等数学二》4月17日专为备考2025年高等数学二考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析:
单选题
1、若x=-1和x=2都是函数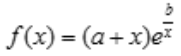 的极值点,则a,b分别为().
的极值点,则a,b分别为().
- A:1,2
- B:2,1
- C:2,-1
- D:-2,1
答 案:B
解 析: 由于x=-1,x=2是函数f(x)的极值点,则有
由于x=-1,x=2是函数f(x)的极值点,则有 .即
.即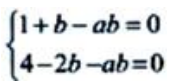 解得a=2,b=1.
解得a=2,b=1.
2、当x→0时,下列为无穷小量的是().
- A:

- B:
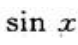
- C:
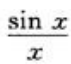
- D:
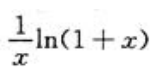
答 案:B
解 析:由无穷小量的定义:若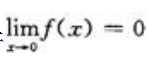 ,则称f(x)为x→0时的无穷小量.而只有
,则称f(x)为x→0时的无穷小量.而只有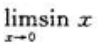 =0.
=0.
主观题
1、设函数z=z(x,y)由sin(x+y)+ez=0确定,求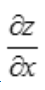 .
.
答 案:解:设F(x,y,z)=sin(x+y)+ez.则 则
则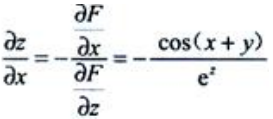
2、己知离散型随机变量X的概率分布为 (1)求常数a;
(1)求常数a;
(2)求X的数学期望EX.
答 案:解:(1)因为0.2+0.1+0.5+a=1,所以a=0.2.(2)EX=10×0.2+20×0.1+30×0.5+40×0.2=27.
填空题
1、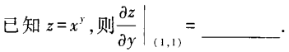
答 案:0
解 析:
2、设函数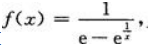 则f(|x+1|)的间断点为()
则f(|x+1|)的间断点为()
答 案:x=1和x=0和x=-2
解 析:由题知,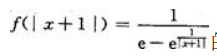 的无定义点为x=1和x=0和x=-2.
的无定义点为x=1和x=0和x=-2.
简答题
1、已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导函数y=f’(x)的图像经过点(1,0)和(2,0)(如图2-1-1所示)。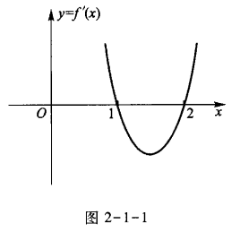
(1)求极值点x0的值;
(2)求a,b,c的值。
答 案:本题考查的知识点是利用导数的图像来判定函数的单调区间和极值点,并以此确定函数的表达式。 (1)在x=1处f’(1)=0,且x<1时,f’(x)>0;1<x<2时,f’(x)<0,可知x=1是极值点,即x0=1。(2)因为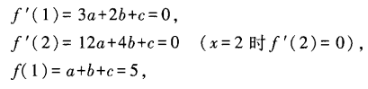 由上面三式解得a=2,b=-9,c=12。
由上面三式解得a=2,b=-9,c=12。
2、求二元函数ƒ(x,y)=x2+y2+xy在条件x+2y=4下的极值。
答 案:解设F((x,y,λ)=ƒ(x,y)+λ(x+2y-4)=x2+y2+xy+λ(x+2y-4),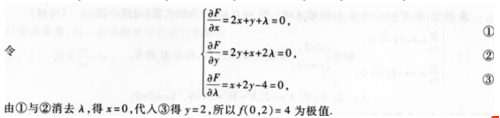
精彩评论