2025年成考高起点每日一练《数学(文史)》4月16日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、如果点A（1，1）和B（2，4）关于直线y=kx+b对称，则k=（）。  

• A：-3
• B：
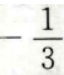
• C：
• D：3

答 案：B

解 析：本题主要考查的知识点为两垂直直线斜率的关系。 直线AB的斜率为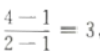：点A、B关于直线y=kx+b对称，因此直线AB与其垂直，故3k=-1，得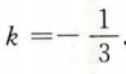

2、已知函数y=f（x）是奇函数，且f（-2）=-6，则f（2）=（）。

• A：-2
• B：6
• C：2
• D：-6

答 案：B

3、袋中有6个球，其中4个红球，2个白球，从中随机取出2个球，则这2个球都为红球的概率为（）

• A：
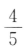
• B：
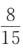
• C：
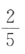
• D：

答 案：C

解 析：两个球都是红球的概率为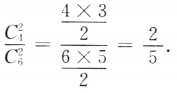

4、若向量a=（x，-2），b=（-2，1），且a//b，则x=（）。

• A：-4
• B：-1
• C：1
• D：4

答 案：D

主观题

1、已知直线l的斜率为1，l过抛物线C：的焦点，且与C交于A,B两点.
(I）求l与C的准线的交点坐标；
(II）求|AB|．

答 案：(I）C的焦点为，准线为由题意得l的方程为因此l与C的准线的交点坐标为(II）由得设A（x1,y1）.B（x2,y2），则因此

2、已知log₅3=a，log₅4=b，求log₂₅12关于a，b的表达式。  

答 案：

3、一艘渔船在航行中遇险，发出警报，在遇险地点西南10海里处有一艘货轮，接收到报时，发现遇险渔船正以9海里/小时的速度与沿南偏东75°方向向某小岛靠近，如果要在40分内将这艘渔船救出，求货轮航行的方向和速度。

答 案：货轮沿东偏北21.8°的方向，以21海里/小时的船速航行。

4、求函数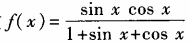（x∈R）的最大值与最小值。  

答 案：设sinx+cosx=t，则（sinx+cosx）²=t²，1+2sinxcosx=t²，sinxcosx= 于是转化为求的最值。 由所设知 上为增函数，故g（t）的最大值为最小值为

填空题

1、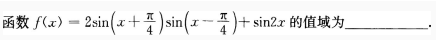  

答 案：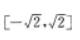

解 析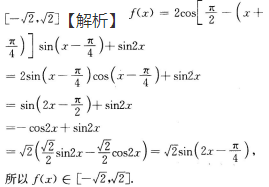： 【考点指要】本题主要考查三角函数的最大值、最小值及值域的求法，解题时需要灵活运用诱导公式、二倍角公式以及辅助角公式，当函数可以化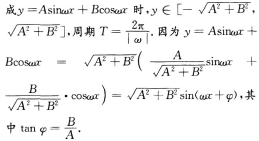

2、在∆ABC中，已知cosA=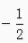，cosB=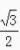，那么cosC=______。

答 案：