2025年成考高起点每日一练《数学(文史)》4月10日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、已知tanα+sinα=m，tanα-sinα=n（m+n≠0），则cosα的值是（）。  

• A：
• B：
• C：
• D：

答 案：A

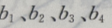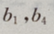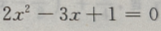2、已知成等差数列，且为方程的两个根，则的值为（）  

• A：
• B：
• C：
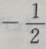
• D：

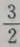
答 案：D

解 析：由根与系数的关系得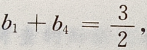由等差数列的性质得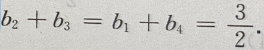

3、设命题甲：x+1=0，命题乙：x²-2x-3=0，则（）。  

• A：甲是乙的充分条件，但不是乙的必要条件
• B：甲是乙的必要条件，但不是乙的充分条件
• C：甲是乙的充分必要条件
• D：甲不是乙的必要条件，也不是乙的充分条件

答 案：A

4、下列函数为奇函数的是 ( )。

• A：
• B：
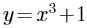
• C：
• D：

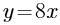
答 案：D

解 析：本题主要考查的知识点为函数的奇偶性．  【应试指导】f(z)=sinx=-sin(-x)=-f(-x)，所以y=sinx为奇函数．        

主观题

1、（1）已知tanα=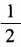 求cot2α的值； （2）已知tan2α=1，求tanα的值。

答 案：（1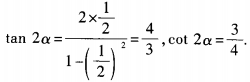） （2）由已知，得 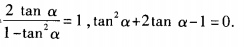解关于tanα的一元二次方程，得tanα=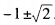

2、已知三角形的一个内角是，面积是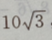周长是20,求各边的长.  

答 案：设三角形三边分别为a,b,c,∠A=60°，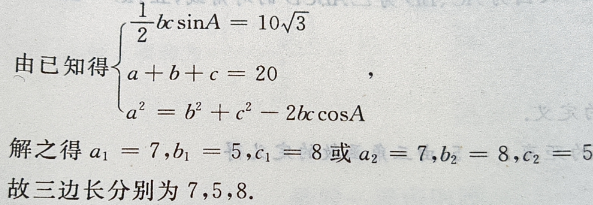  

3、若tanα、tanβ是关于x的方程mx²-(2m-3)x+m-2=0的两个实根，求tan(α+β)的取值范围

答 案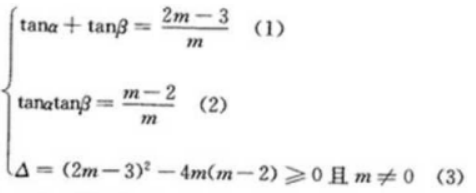： 由(1)(2)得，tan(a+β)=m-3/2;由(3)得m≤9/4且m≠0所以tan(a+β)的取值范围是(-∞，-3/2)U(-3/2，3/4)  

4、设函数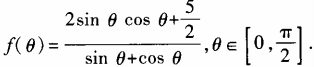 （1）求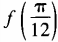；（2）求函数f（θ）最小值。

答 案：

填空题

1、log₂[log₂（log₃81）]=______。  

答 案：1

解 析：由于log₃81=log₃3⁴=4，于是 原式=log₂（log₂4）=log₂2=1。  

2、已知tanθ=1/2，则sin2θ+sin2θ=__________．

答 案：1

解 析：