2025年成考专升本每日一练《高等数学二》4月9日专为备考2025年高等数学二考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

判断题

1、若，则。（）  

答 案：错

解 析：

单选题

1、设函数z＝e^x＋y²，则（）.

• A：2y
• B：e^x＋2y
• C：e^x＋y²
• D：e^x

答 案：D

解 析：当对x求导时，y相当于常量，故，.

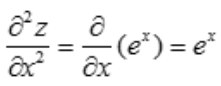2、设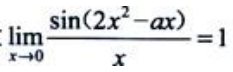,则a＝（）.

• A：-1
• B：-2
• C：1
• D：2

答 案：A

解 析：，所以a＝-1.

主观题

1、（1）求在区间[0，π]上的曲线y＝sinx与x轴所围成图形的面积A；（2）求（1）中的平面图形绕x轴旋转一周所得旋转体的体积V_x．

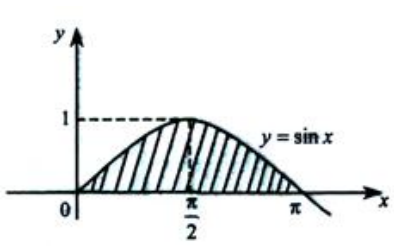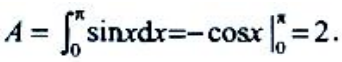答 案：解：平面图形如下图阴影部分．（1）（2）

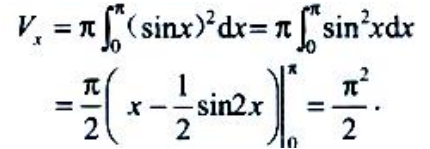
2、某商店库存100台相同型号的冰箱待售，其中有60台是甲厂生产的，有25台是乙厂生产的，有15台是丙厂生产的．这三个厂生产的冰箱不合格率分别为：0.1，0.4，0.2；一顾客从这批冰箱中随机地买了1台，开机测试后发现是不合格冰箱，由于厂标已脱落，试问这台冰箱最有可能是哪个厂生产的？

答 案：解：设B＝{顾客买的冰箱不合格），A₁＝{甲厂生产的冰箱），A₂＝（乙厂生产的冰箱}，A₃＝（丙厂生产的冰箱）．由题意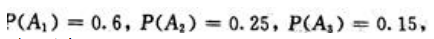，且A₁，A₂，A₃相互独立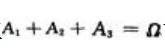故，由贝叶斯公式得，顾客买不合格的冰箱是甲厂生产的概率为：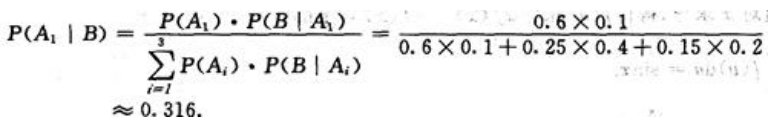
同理，不合格品是乙厂生产的概率为：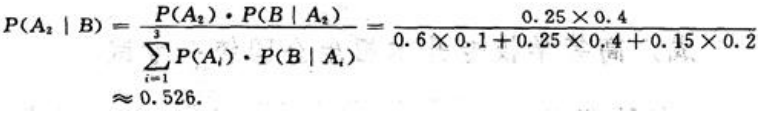
不合格品是丙厂生产的概率为：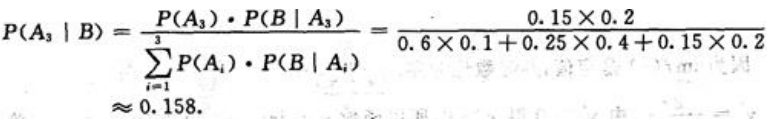
比较上述三个数据知，这台不合格冰箱最有可能是乙厂生产的．

填空题

1、_________。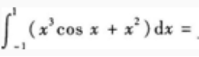  

答 案：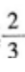

解 析：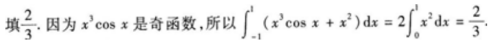

2、（）．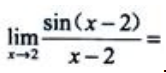

答 案：1

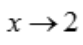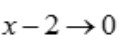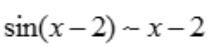解 析：由等价无穷小可知，时，即，，故．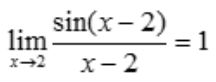

简答题

1、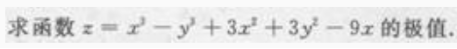  

答 案：

2、计算  

答 案：由洛必达法则有