2025年高职单招每日一练《数学(中职)》5月27日专为备考2025年数学(中职)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、已知等比数列{an}中,a2=9,a5=243,则{an}的前4项和S4为()
- A:81
- B:120
- C:168
- D:192
答 案:B
解 析:设等比数列{aa|的公比为q.因为a2=9,a5=243,所以a5=a2q3=9q³=243,解得q=3.又a2=9,所以a1=3,所以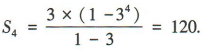
2、从4名男生和2名女生中选2人参加会议,至少有1名男生,不同的安排方法的种数为()
- A:13
- B:14
- C:15
- D:16
答 案:B
解 析:根据题意,从4名男生和2名女生中选2人参加会议,有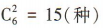 选法,没有男生,即全部为女生的选法有
选法,没有男生,即全部为女生的选法有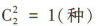 ,则至少有1名男生的选法有15-1=14(种).
,则至少有1名男生的选法有15-1=14(种).
3、从 1,2,3,4,5中任选3个数,从7,8,9中任选2个数,可组成无重复数字的五位数的个数为()
- A:2 400
- B:3 600
- C:90
- D:180
答 案:B
解 析:先从1,2,3,4,5中任选3个数,方法有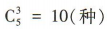 ;再从7,8,9中任取2个数字,方法有
;再从7,8,9中任取2个数字,方法有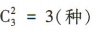 ;最后把这5个数组成无重复数字的五位数,方法有
;最后把这5个数组成无重复数字的五位数,方法有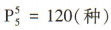 .根据分步乘法计数原理可得它们可组成无重复数字的五位数的个数为 10x3x120 =3 600.
.根据分步乘法计数原理可得它们可组成无重复数字的五位数的个数为 10x3x120 =3 600.
主观题
1、已知
答 案:方法一:矢量图表示法 矢量图表示法如图所示。
 方法二:矢量表示法
方法二:矢量表示法
解 析:


填空题
1、已知数列{an}为等差数列,且 a1+ a7+a13=2π,则 tan a7=()
答 案: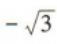
解 析: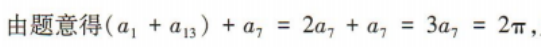
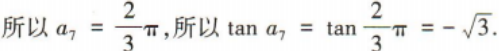
2、cos45°cos15°+sin45°sin15°= ___________________
答 案:2√3
解 析: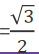 cos45°cos15°+sin45°sin15°
= cos(45°-15°)
= cos30°
cos45°cos15°+sin45°sin15°
= cos(45°-15°)
= cos30°
3、(1+x)5的展开式中,二项式系数的和是()
答 案:32
解 析:令x=1,得二项式系数的和为25= 32.
简答题
1、在等比数列{an}中,a1a2a3=8,a2+a4=10. (1)求首项a1及公比q; (2)求该数列的前8项和S8
答 案:
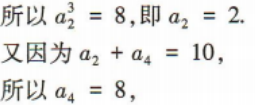

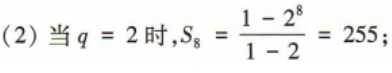
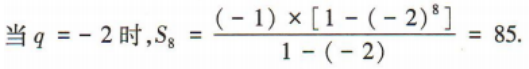
精彩评论