2025年高职单招每日一练《数学(中职)》5月23日专为备考2025年数学(中职)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、已知椭圆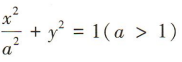的左、右焦点分别为F₁,F₂过点F₁的直线l交椭圆于 A,B两点.若△ABF₂的周长为8.则a=()  

• A：4
• B：
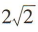
• C：2
• D：

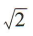
答 案：C

解 析：根据椭圆的定义可得△ABF₂的周长为|AF₁|+|AF₂|+|BF₁|+|BF₂|=2a+2a= 4a=8,所以a = 2.

2、过圆x²+y²=25 上一点 P(3,4)的切线方程为（）  

• A：3x+4y-25 =0
• B：3x+4y+25 =0
• C：3x-4y-25=0
• D：3x-4y+25=0

答 案：A

解 析：易得圆x²+y²=25的圆心坐标为O(0,0).又因为点 P(3,4),直线OP的斜率为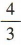,所以圆x²+y²=25在点P处的切线的斜率为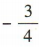,所以该切线的方程为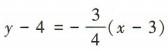,即3x+4y-25=0.

3、sin750°=（）

• A：
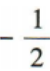
• B：
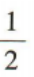
• C：
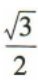
• D：

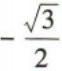
答 案：B

解 析：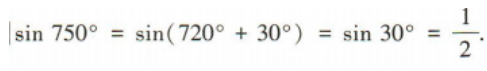

主观题

1、已知

答 案：方法一：矢量图表示法 矢量图表示法如图所示。 方法二：矢量表示法

解 析：

填空题

1、当x>2时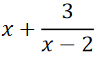，的最小值为____________

答 案：

解 析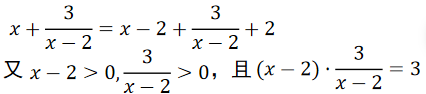： 是定值，  故由均值定理得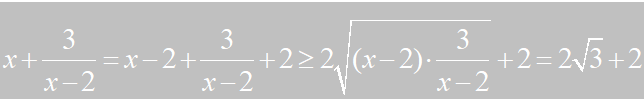，  当且仅当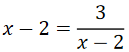 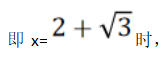有最小值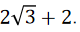

2、某学校计划从5名女生,3名男生中选出4人参加数学竞赛,则选出的4人为2名女生和2名男生的选法有（）种.  

答 案：30

解 析：从5名女生,3名男生中选出2名女生和2名男生的不同选法有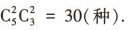

3、(1-2x)³的展开式中系数最大的项是（）  

答 案：12x²

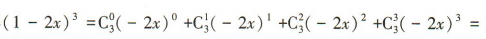
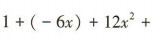
解 析：将(1-2x)³展开得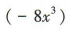,所以系数最大的项为12x².

简答题

1、平行四边形ABCD中，BD=2√3,AB=2,AD=4,将△CBD沿对角线BD折到△EBD,使得平面CBD丄平面ABD，求证：AB丄DE.  

答 案：证明: 在△ABD中，AB=2,AD=4,BD=2√3 则AB²+BD²=AD²，故AB⊥BD， 又平面EBD⊥平面ABD，交线为BD，而AB⊥BD 故AB⊥平面EBD, 则AB⊥DE.