2025年高职单招每日一练《数学》5月20日专为备考2025年数学考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

判断题

1、各边相等的多边形是正多边形。（）  

答 案：错

解 析：菱形的各边相等，但它不一定是正方形。

2、设集合A={a,b,c},B={c,d},则AUB={a,b,c,d}。（）  

答 案：对

解 析：AUB为集合A和集合B合并到一起

单选题

1、设a=log_0.32，b=0.2^0.3，c=3^0.2，则a，b，c的大小关系是（　　）

• A：a
• B：a
• C：b
• D：c

答 案：A

解 析：对数值大小的比较 专题：函数的性质及应用 分析：利用指数函数与对数函数的单调性即可得出． ∵a=log0.32＜0，0＜b=0.20.3，＜1，c=30.2＞1．∴a＜b＜c．故选：A． 点评：本题考查了指数函数与对数函数的单调性，属于基础题．

2、将2名教师，4名学生分成2个小组，分别安排到甲、乙两地参加社会实践活动，每个小组由1名教师和2名学生组成，不同的安排方案共有()  

• A：12种
• B：10种
• C：9种
• D：8种

答 案：A

多选题

1、已知等差数列{a_n}的前n项和为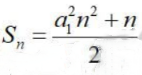，公差为d，则（）  

• A：a₁=1
• B：d=1
• C：
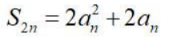
• D：2S_n-a_n=1+3+5+...+(2n-1)

答 案：ABD

2、下列四个命题中正确的是（）  

• A：与圆有公共点的直线是该圆的切线
• B：垂直于圆的半径的直线是该圆的切线
• C：到圆心的距离等于半径的直线是该圆的切线
• D：过圆直径的端点，垂直于此直径的直线是该圆的切线

答 案：CD

解 析：A中，与圆有两个公共点的直线，是圆的割线，故该选项不符合题意；B中，应经过此半径的外端，故该选项不符合题意；C中，根据切线的判定方法，故该选项符合题意；D中，根据切线的判定方法，故该选项符合题意。故选：CD。

主观题

1、已知函数f(x)=log₃(3x—1).(1)求函数f(x)的定义域；
(2)若f(x)<1,求x的取值范围.

答 案：(1)根据题意可得，3x-1>0,解得所以函数f(x)的定义域是(2)因为f(x)=log₃(3x-1)<1=log₃3,f(x)为定义域上的增函数，所以O<3x-1<3,解得所以x的取值范围是

2、如图所示，在平面四边形ABCD中，AB=√5,AC=3,BC=2√2. 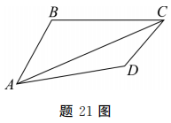(1)求∠ACB的大小； (2)若cos∠ADC=,cos∠BCD=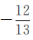,求线段AD的长.  

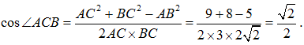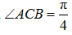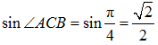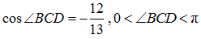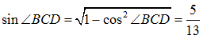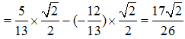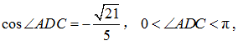答 案：（1）在△ABC中，由余弦定理得 因为0＜∠ACB＜π，所以 （2）由（1）可知 因为，所以 Sin∠ACD=sin(∠BCD-∠ACB)=sin∠BCDcos∠ACB-cos∠BCDsin∠ACB 又因为 所以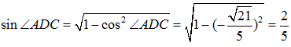 在△ACD中，由正弦定理得 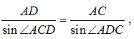所以  

填空题

1、已知函数f(x)与g(x)的图像关于y轴对称，且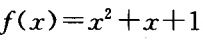,则g(x)=______。  

答 案：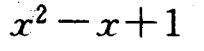

2、  

答 案：160°；二