2025年高职单招每日一练《数学》5月15日专为备考2025年数学考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
判断题
1、高三某班共有学生56人,其中女生24人,现用分层抽样的方法,选取14人参加一项活动,则应选取女生6人.()
答 案:对
解 析:由题意知,应选取女生人数为:14/56×24=6
2、任何一个集合至少有两个子集()。
答 案:错
解 析:当集合为空集时,只有一个子集,所以错误。
单选题
1、五个关系式: 。其中正确的个数为()
。其中正确的个数为()
- A:6
- B:5
- C:4
- D:3
答 案:C
解 析:
2、为了解全年级1180名学生的数学成绩分别情况,在一次数学调研测试后,某教师随机抽取了80份试卷并对试卷得分(满分:150分)进行了整理,得到如下频率分布表:
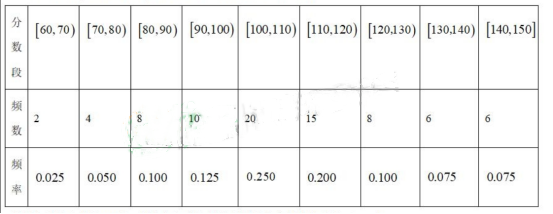 若规定及格分数是90分,则全年级此次的数学测试的及格率的估计值是()
若规定及格分数是90分,则全年级此次的数学测试的及格率的估计值是()
- A:70%
- B:72.5%
- C:80%
- D:82.5%
答 案:D
多选题
1、下列关系式正确的是()
- A:
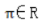
- B:-5∈Z
- C:
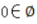
- D:1/2∈Q
答 案:ABD
解 析:A:R是实数,为有理数和无理数。B:在数学里用大写符号Z表示全体整数的集合,包括正整数、0、负整数。D:Q是有理数的集合。C:空集是没有任何元素的,因此也不会有元素0,因此C选项错误,ABD正确。
2、下列四个命题中正确的是()
- A:与圆有公共点的直线是该圆的切线
- B:垂直于圆的半径的直线是该圆的切线
- C:到圆心的距离等于半径的直线是该圆的切线
- D:过圆直径的端点,垂直于此直径的直线是该圆的切线
答 案:CD
解 析:A中,与圆有两个公共点的直线,是圆的割线,故该选项不符合题意;B中,应经过此半径的外端,故该选项不符合题意;C中,根据切线的判定方法,故该选项符合题意;D中,根据切线的判定方法,故该选项符合题意。故选:CD。
主观题
1、如图所示,在三棱锥P-ABC中,PB⊥平面ABC,AB⊥AC,垂足为点A
(1)证明:AC⊥平面PAB;
(2)若AC=3,BC=√10,直线PC与平面PAB所成的角为30°,求三棱锥B-PAC的体积.
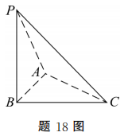
答 案:(1)证明:因为PB⊥平面ABC,AC⊆平面ABC,所以PB⊥AC 又因为AB⊥AC,AB,PB⊆平面PAB,AB∩PB=B,
所以AC⊥平面PAB
(2)因为直线PC与平面PAB所成的角为30°,AC⊥平面PAB,
所以在直角三角形PAC中,∠CPA=30°,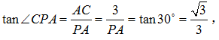 解得PA=3√3
又因为△ABC的面积
解得PA=3√3
又因为△ABC的面积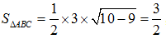 ,PB⊥平面ABC
,PB⊥平面ABC
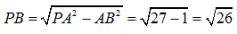 所以
所以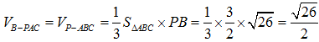
2、设函数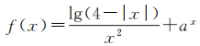 ,a>0且a≠1.
(1)求函数f(x)的定义域;
(2)若f(-3)=8,求实数a的值,并判断函数f(x)的奇偶性.
,a>0且a≠1.
(1)求函数f(x)的定义域;
(2)若f(-3)=8,求实数a的值,并判断函数f(x)的奇偶性.
答 案:(1)由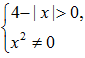 ,得
,得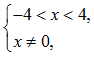 即有-4<x<0或0<x<4
因此,函数f(x)的定义域为{x|-4<x<0或0<x<4}
(2)因为
即有-4<x<0或0<x<4
因此,函数f(x)的定义域为{x|-4<x<0或0<x<4}
(2)因为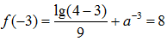 所以
所以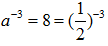 ,解得
,解得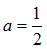 因为
因为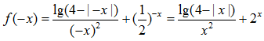 所以f(-x)≠-f(x),且f(-x)≠f(x).
因此,函数f(x)既不是奇函数也不是偶函数
所以f(-x)≠-f(x),且f(-x)≠f(x).
因此,函数f(x)既不是奇函数也不是偶函数
填空题
1、
设 x,y∈R,且 x+y=5,则3x+ 3y的最小值是_____。
答 案:
解 析:
2、a、b、c是同一平面内的三条直线,且a//b,b⊥c,则a与c的位置关系是______
答 案:垂直
精彩评论