2025年成考高起点每日一练《数学(文史)》4月30日专为备考2025年数学(文史)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、二次函数y=x2+4x+1()。
- A:有最小值-3
- B:有最大值-3
- C:有最小值-6
- D:有最大值-6
答 案:A
2、已知x+x-1=2cos40°,则x4+x-4=()。
- A:2cos20°
- B:-2cos20°
- C:2sin80°
- D:-2sin80°
答 案:B
解 析:由已知得(x+x-1)2=(2 cos 40°)2,x2+2+x-2=4cos240° x2+x-2=2(2 cos240°-1)= 2cos 80°同样可得x4+x-4=2 cos 160°=-2 cos 20°故选B。
3、已知向量a=(3,1),b=(-2,5),则3a-2b=()。
- A:(2,7)
- B:(13,-7)
- C:(2,-7)
- D:(13,,13)
答 案:B
解 析:根据a=(3,1),b=(-2,5),则3a-2b=3×(3,1)-2×(-2,5)=(13,-7)
4、函数y=-x2+2x的值域是()。
- A:[0,+∞)
- B:[1,+∞)
- C:(-∞,1]
- D:(-∞,0)
答 案:C
解 析:本题主要考查的知识点为函数的值域. y=-x2+2x=1-(x-1)2≤1,故原函数的值域为(-∞,1]
主观题
1、在△ABC中,已知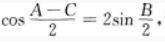 证明a,b,c成等差数列。
证明a,b,c成等差数列。
答 案: 考点 本题主要考查三角函数的恒等变换以及积化和差公式的应用,积化和差有一定难度,请考生注意.
考点 本题主要考查三角函数的恒等变换以及积化和差公式的应用,积化和差有一定难度,请考生注意.
2、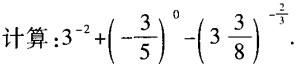
答 案:
3、已知等差数列 前n项和
前n项和 (Ⅰ)求通项
(Ⅰ)求通项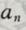 的表达式
(Ⅱ)求
的表达式
(Ⅱ)求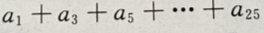 的值
的值
答 案:(Ⅰ)当n=1时,由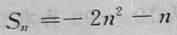 得
得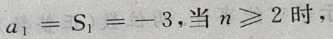
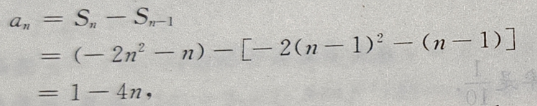
 也满足上式,故
也满足上式,故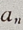 =1-4n(n≥1)
(Ⅱ)由于数列
=1-4n(n≥1)
(Ⅱ)由于数列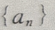 是首项为
是首项为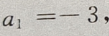 公差为d=-4的等差数列,所以
公差为d=-4的等差数列,所以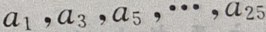 是首项为
是首项为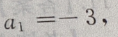 公差为d=-8,项数为13的等差数列,于是由等差数列前n项和公式得:
公差为d=-8,项数为13的等差数列,于是由等差数列前n项和公式得:

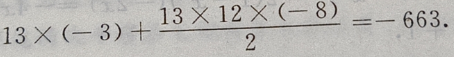
4、等差数列{an}的通项公式为an=3n-1,在{an}中,每相邻的两项之间插人三项,构成新的等差数列{bn}. (Ⅰ)求{bn}的通项公式; (Ⅱ)求{bn}前10项的和.
答 案: 考点本题主要考查等差数列的通项公式和前n项和公式的运用,是成人高考常见题型.
考点本题主要考查等差数列的通项公式和前n项和公式的运用,是成人高考常见题型.
填空题
1、化简sin(x+y)-2cosxsiny=______。
答 案:sin(x-y)
解 析:原式=sinxcosy+cosxsiny-2cosxsiny=sinxcosy-cosxsiny=sin(x-y)
2、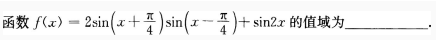
答 案: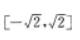
解 析: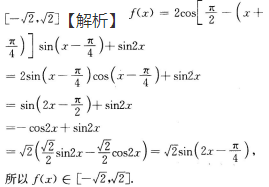 【考点指要】本题主要考查三角函数的最大值、最小值及值域的求法,解题时需要灵活运用诱导公式、二倍角公式以及辅助角公式,当函数可以化
【考点指要】本题主要考查三角函数的最大值、最小值及值域的求法,解题时需要灵活运用诱导公式、二倍角公式以及辅助角公式,当函数可以化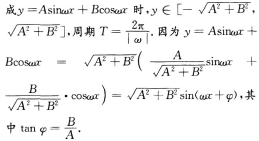
精彩评论