2025年成考高起点每日一练《数学(文史)》4月29日专为备考2025年数学(文史)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、已知向量|a|=3,|b|=4,且a和b的夹角为120°,则a·b=()。
- A:
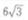
- B:
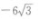
- C:6
- D:-6
答 案:D
2、6本不同的语文书和4本不同的数学书,任意排放在书架上,则4本数学书放在一起的概率是()。
- A:
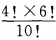
- B:
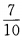
- C:
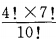
- D:

答 案:C
解 析:此题属于等可能事件的概率(即古典概率),6本不同的语文书和4本不同的数学书任意排放在书架上的排列数就为基本事件的总数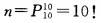 4本数学书排在一起的排列数为
4本数学书排在一起的排列数为 ,所以4本数学书放在一起的概率为
,所以4本数学书放在一起的概率为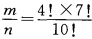 ,故应选C。
,故应选C。
3、已知f(x)=ax2+b的图像经过点(1,2)且其反函数f-1(x)图像经过点(3,0),则函数f(x)的解析式是()。
- A:
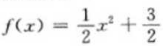
- B:f(x)=-x2+3
- C:f(x)=3x2+2
- D:f(x)=x2+3
答 案:B
解 析:∵f(x)的反函数f-1(x)过点(3,0),所以f(x)又过点(3,0),所以有f(1)=2,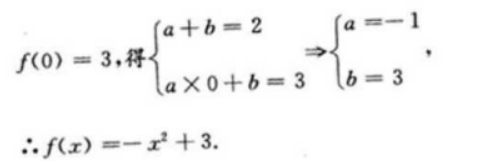
4、下列函数在定义域内,既是奇函数又是增函数的是()。
- A:y=sinx
- B:y=log2x
- C:y=x+8
- D:y=x3
答 案:D
主观题
1、已知tan2θ=2tan2ψ+1,求cos2θ+sin2ψ的值。
答 案:由已知,得 
2、已知直线l的斜率为1,l过抛物线C: 的焦点,且与C交于A,B两点.
的焦点,且与C交于A,B两点.
(I)求l与C的准线的交点坐标;
(II)求|AB|.
答 案:(I)C的焦点为 ,准线为
,准线为 由题意得l的方程为
由题意得l的方程为 因此l与C的准线的交点坐标为
因此l与C的准线的交点坐标为 (II)由
(II)由 得
得 设A(x1,y1).B(x2,y2),则
设A(x1,y1).B(x2,y2),则 因此
因此
3、求(1+tan10°)(1+tan35°)的值。
答 案:原式=1+tan10°+tan35°+tan10°·tan35° 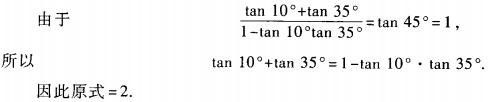
4、求下列函数的最大值、最小值和最小正周期: (1)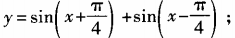 2)y=6cosx+8sinx
2)y=6cosx+8sinx
答 案: 所以函数的最大值是
所以函数的最大值是 最小值是
最小值是 最小正周期为2π,
(2)要将6cosx+8sinx化为sinαcosx+cosαsinx这种形式,需使cosx与sinx的系数平方和为1,为此,将已知函数化为
最小正周期为2π,
(2)要将6cosx+8sinx化为sinαcosx+cosαsinx这种形式,需使cosx与sinx的系数平方和为1,为此,将已知函数化为 因此,函数的最大值是10,最小值是-10,最小正周期为2π
因此,函数的最大值是10,最小值是-10,最小正周期为2π
填空题
1、log2[log2(log381)]=______。
答 案:1
解 析:由于log381=log334=4,于是 原式=log2(log24)=log22=1。
2、任选一个不大于20的正整数,它恰好是3的整数倍的概率是()
答 案: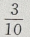
解 析:设n为不大于20的正整数的个数,则n=20,m为在这20个数中3的倍数:3,6、9、12、15、18的个数。 ∴m=6,∴所求概率=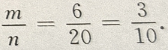
精彩评论