2025年成考高起点每日一练《数学(理)》4月29日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、下列函数中为奇函数的是()。
- A:y=2lgx
- B:y=3x+3-x
- C:y=x3+sin2x
- D:y=x3+tanx
答 案:D
解 析:对于D,f(-x)=(-x)3+tan(-x)=-(x3+tanx)=-f(x)。答案为D。
2、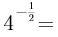 ( )
( )
- A:-2
- B:
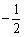
- C:
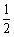
- D:2
答 案:C
3、在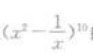 的展开式中,含x5项的系数是()。
的展开式中,含x5项的系数是()。
- A:1
- B:-1
- C:252
- D:-252
答 案:D
解 析: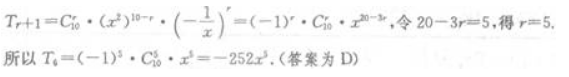
4、两条直线是异面直线的充分条件是这两条直线()。
- A:分别在两个平面内
- B:是分别在两个相交平面内的不相交的直线
- C:是分别在两个相交平面内的不平行的直线
- D:分别在两个相交平面内,其中一条与这两个平面的交线相交于一点,而另一条不过这个点
答 案:D
主观题
1、已知am=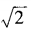 ,an=
,an=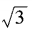 ,求a3n-4m的值。
,求a3n-4m的值。
答 案: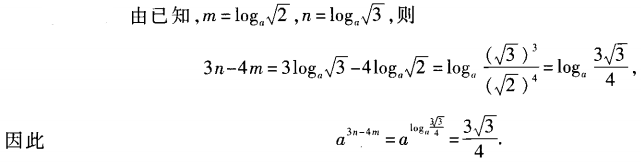
2、在△ABC中,B=120°,BC=4,△ABC的面积为 ,求AC.
,求AC.
答 案:由△ABC的面积为 得
得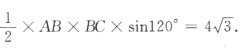 所以AB =4.因此
所以AB =4.因此 所以
所以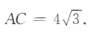
3、当自变量为何值时,函数y=2x3-3x2-12x+21有极值,其极值为多少?
答 案:y'=6x2-6x-12=6(x-2)(x+1) 当x<-1或x>2时,y>0,当-1
4、试证明下列各题
(1)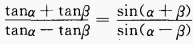
(2)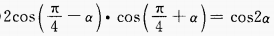
答 案:(1)化正切为正、余弦,通分即可得证。 (2)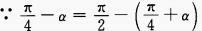

填空题
1、一个问题在1小时内,甲能独立解决的概率是0.5,乙能独立解决的概率是0.4,两人在1小时内解决问题的概率是______。
答 案:0.7
解 析:设事件A为两人在1小时内解决问题,即1小时内至少有一人能解决问题,事件B为甲在1小时内解决问题,事件C为乙在1小时内解决问题,事件B、C是相互独立事件,事件A的对立事件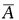 互为在1小时内两个人都没有解决问题,所以 P(A)=1-P(
互为在1小时内两个人都没有解决问题,所以 P(A)=1-P(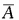 )=1-P(
)=1-P(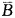 ·
·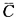 )=1-P(
)=1-P(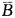 )·P(
)·P(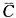 )
=1-(1-0.5)×(1-0.4)=1-(0.5×0.6)=1-0.3=0.7
)
=1-(1-0.5)×(1-0.4)=1-(0.5×0.6)=1-0.3=0.7
2、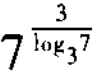 =______。
=______。
答 案:27
解 析: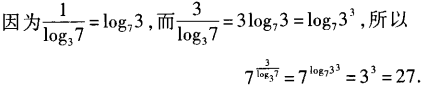
精彩评论