2025年高职单招每日一练《数学》4月27日专为备考2025年数学考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

判断题

1、甲、乙两台机床，它们因故障停机的概率分别为0.01和0.02，则这两台机床同时因故障停机的概率为0.03。（）  

答 案：错

2、将函数y=sinx的图像沿着x轴方向向右平移π/3个单位，便可得到函数y=sin(x-π/3)的图像。（）  

答 案：对

解 析：

单选题

1、如图是某地一的长方形大理石广场示意图，如果小琴要从A角走到C角，至少走____米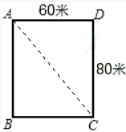  

• A：90
• B：100
• C：120
• D：140

答 案：B

解 析：由于两点之间线段最短，因此小红所走的最短距离实际是AC的长；根据矩形的性质知△ACD是直角三角形，已知了两条直角边的长，即可由勾股定理求出斜边AC的长． ∵四边形ABCD是矩形， ∴∠D=90°， Rt△ACD中，AD=60m，CD=80m， 根据勾股定理，得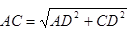=100m ， 故选B.

2、不等式|x|>3的解集是()  

• A：x>3
• B：x<-3
• C：x>3或x<-3
• D：-3

答 案：C

解 析：当x为负值时|x|=-x，则|x|>3为-x>3即为x<-3，当x为正值时|x|=x，则|x|>3为x>3，综上，不等式|x|>3的解集是x>3或x<-3

多选题

1、下列说法不正确的是（）  

• A：相切两圆的连心线经过切点
• B：长度相等的两条弧是等弧
• C：平分弦的直径垂直于弦
• D：相等的圆心角所对的弦相等

答 案：BCD

解 析：A、根据圆的轴对称性可知此命题正确，不符合题意；B、等弧指的是在同圆或等圆中，能够完全重合的弧．而此命题没有强调在同圆或等圆中，所以长度相等的两条弧，不一定能够完全重合，此命题错误，符合题意；C、此弦不能是直径，命题错误，符合题意；D、相等的圆心角指的是在同圆或等圆中，此命题错误，符合题意；故选：BCD

2、设等差数列{a_n}的公差为d，其前n项和为S_n，且a₁=-5，S₃=-9，则（）  

• A：d=2
• B：S₂，S₄，S₆为等差数列
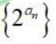• C：数列是等比数列
• D：S₃是S_n的最小值

答 案：ACD

主观题

1、已知两直线,当m为何值时，l₁与l₂: (1)相交；(2)平行；(3)重合.  

答 案：(1)当1×3m-(m-2)m²=-m²(m-2)+3m=-m(m-3)(m+1)≠0时，l₁与l₂相交，即m≠0,m≠3且m≠-1. (2)当-m(m-3)(m+1)=0且1×2m-(m-2)×6=12-4m≠0时，l₁与l₂平行，即m=0或m=-1. (3)当-m(m-3)(m+1)=0且12-4m=0时，l₁与l₂重合，即m=3.

2、已知函数f(x)=log₃(3x—1).(1)求函数f(x)的定义域；
(2)若f(x)<1,求x的取值范围.

答 案：(1)根据题意可得，3x-1>0,解得所以函数f(x)的定义域是(2)因为f(x)=log₃(3x-1)<1=log₃3,f(x)为定义域上的增函数，所以O<3x-1<3,解得所以x的取值范围是

填空题

1、若a>b>0,则a(a+b)（）a².(填“>”“<”或“=”)

答 案：>

解 析：因为a(a+b)=a²+ab,又因为a>b>0,即ab>0,所以a(a+b)>a².

2、已知函数f(x)是定义在R上的奇函数，当x∈ (-∞，0)时，f (x) =2x³+x²,所以f(2) =（）  

答 案：12

解 析：.当x∈ (-∞，0)时，f (x) =2x³+x²,所以f( -2) =- 12,又因为函数f (x)是定义在 R上的奇函数所以f (2) =12,故答案为:12