2025年高职单招每日一练《数学(中职)》4月25日专为备考2025年数学(中职)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、已知圆M经过A(1,0),B(3,0),C(0,1)三点,则圆M的标准方程为()
- A:(x-2)²+(y-2)²=5
- B:(x-2)²+(y+2)²=5
- C:(x+2)²+(y-2)²=5
- D:(x+2)²+(y+2)²=5
答 案:A
解 析:因为圆M经过A(1,0),B(3,0),所以圆心M在直线x=2上,故设圆心为M(2,b),又|MA|=|MC|,所以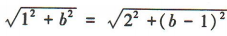 ,解得b=2,所以半径
,解得b=2,所以半径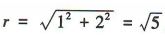 ,则圆M的标准方程为(x-2)²+(y-2)²=5。
,则圆M的标准方程为(x-2)²+(y-2)²=5。
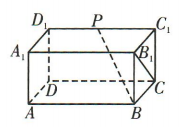
2、如图,在长方体ABCD-A₁B₁C₁D₁中,BB₁=BC,P为C₁D₁的中点,则异面直线PB与B₁C所成角的大小为()
- A:30°
- B:45°
- C:60°
- D:90°
答 案:D
解 析:连接BC1,AD1.在长方体ABCD-A1B1C1D1中,由BB1=BC得侧面BCC1B1是正方形,所以BC1⊥B1C.由D1C1⊥平面BCC1B1,B1C⊂平面BCC1B1,得D1C1⊥B1C.又D1C1∩BC1=C1,D1C1⊂平面ABC1D1,BC1⊂平面ABC1D1,所以B1C1⊥平面ABC1D1,又BP⊂平面ABC1D1,所以B1C⊥BP,即异面直线PB与B1C所成角的大小为90°。
3、不等式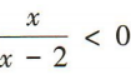 的解集为()
的解集为()
- A:[0,2]
- B:(0,2]
- C:(-∞,0)∪[2,+∞)
- D:(0,2)
答 案:D
解 析: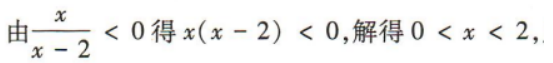
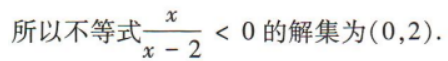
主观题
1、已知
答 案:方法一:矢量图表示法 矢量图表示法如图所示。
 方法二:矢量表示法
方法二:矢量表示法
解 析:


填空题
1、如图所示的表被称为“杨辉三角”,则在“杨辉三角”中,从上往下第10行的数字之和为().(用数字作答)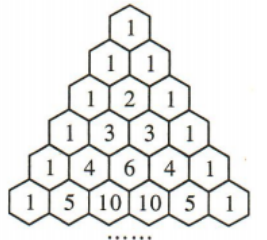
答 案:512
解 析:第1行只有一个数字1,即20,第2行的数字之和为21,第3行的数字之和为22,…,以此类推,第1行数字与从第2行起,每行的数字之和构成首项为1,公比为2的等比数列,则第10行的数字之和为29=512.
2、若函数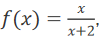 则
则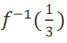 = _______
= _______
答 案:1
解 析:解法一:
由 得
得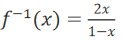 ∴
∴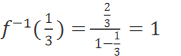 解法二:
由
解法二:
由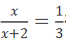 得x=1
∴
得x=1
∴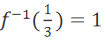
3、不等式|2x-3|<5的解集为______________
答 案:{x|-1 解 析:不等式|2x-3|<5,
可化为-5<2x-3<5,
解得:-1 简答题 1、已知m∈R,命题 答 案:若命题p为真命题,则m2-3m≤(x2-2x-1)min, 因为x∈[0,1],
所以(x2-2x-1)min=-2,
所以m2-3m≤-2,解得1≤m≤2,所以m的取值范围为[1,2]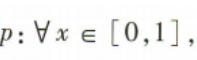 不等式m2-3m≤x2-2x-1恒成立.若p为真命题,求实数m的取值范围.
不等式m2-3m≤x2-2x-1恒成立.若p为真命题,求实数m的取值范围.
精彩评论