2025年成考高起点每日一练《数学(理)》4月9日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、抛物线y＝ax²（a＜0）的焦点坐标是（）。

• A：
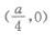
• B：
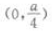
• C：
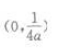
• D：

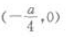
答 案：C

解 析：

2、在△ABC中，若lgsinA-lgsinB-lgcos=lg2，则△ABC是（）

• A：以A为直角的三角形
• B：b=c的等腰三角形
• C：等边三角形
• D：钝角三角形

答 案：B

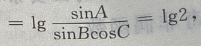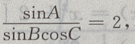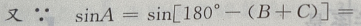
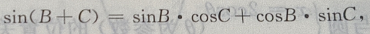
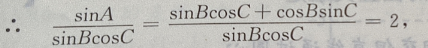
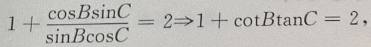
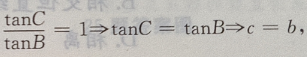解 析：判断三角形的形状，条件是用一个对数等式给出先将对数式利用对数的运算法则整理。 ∵lgsinA-lgsinB-lgcos=lg2，由对数运算法则可得,左 两个对数底数相等则真数相等：即2sinBcosC=sinA 在△ABC中，∵A+B+C=180°，∴A=180°-（B+C）, 故为等腰三角形

3、设log₅7＝m，log₂5＝n，则log₂7＝（）。

• A：
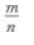
• B：
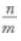
• C：m＋n
• D：m·n

答 案：D

解 析：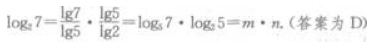

4、在等比数列{an}中，a2=1，公比q=2，则a5=（）。

• A：
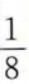
• B：
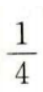
• C：4
• D：8

答 案：D

解 析：本题主要考查的知识点为等比数列。

主观题

1、在△ABC中如果sinA=2sinBcosC，求证：△ABC是等腰三角形。  

答 案：∴△ABC为等腰三角形。

2、已知直线l的斜率为1，l过抛物线C：的焦点，且与C交于A,B两点.(I）求l与C的准线的交点坐标；
(II）求|AB|.

答 案：(I）C的焦点为，准线为由题意得l的方程为因此l与C的准线的交点坐标为(II）由，得设A（x1,y1），B（x2,y2），则因此

3、（1）已知tanα=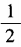，求cot2α的值； （2）已知tan2α=1，求tanα的值。

答 案：（1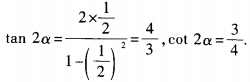）（2）由已知，得 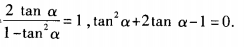解关于tanα的一元二次方程，得tanα=  

4、求下列函数的最大值、最小值和最小正周期： （1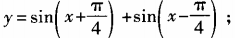）（2）y=6cosx+8sinx

答 案：  

填空题

1、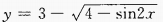的值域是______。  

答 案：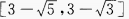

解 析：当sin2x=-1时，y最小值当 sin2x=1时,  

2、函数y=x⁴-2x²+5,x∈[-2,2]上的最小值______，最大值______。

答 案：4；13

解 析：y=x⁴-2x²+5,y'=4x³-4x