2025年成考高起点每日一练《数学(理)》3月27日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、已知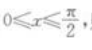 则函数 y=sinx+cosx的值城为()。
则函数 y=sinx+cosx的值城为()。
- A:[-1,1]
- B:
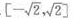
- C:
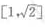
- D:
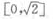
答 案:C
2、一部电影在4个单位轮映,每一单位放映一场,轮映次序有()。
- A:4种
- B:16种
- C:24种
- D:256种
答 案:C
3、抛物线y2=2px上任意一点与焦点连线中点的轨迹方程是()。
- A:
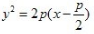
- B:
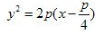
- C:

- D:
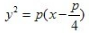
答 案:D
4、(sinα+sinβ)2+(cosα+cosβ)2=()。
- A:
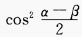
- B:
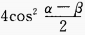
- C:
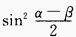
- D:
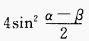
答 案:B
解 析: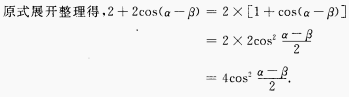
主观题
1、在正四棱柱ABCD-A'B'C'D'中, (Ⅰ)写出向量
(Ⅰ)写出向量 关于基底{a,b,c}的分解式
(Ⅱ)求证:
关于基底{a,b,c}的分解式
(Ⅱ)求证: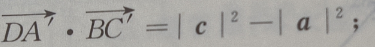 (Ⅲ)求证:
(Ⅲ)求证: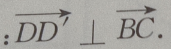
答 案:(Ⅰ)由题意知(如图所示) 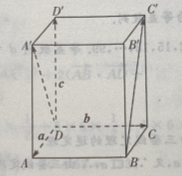
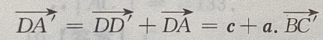
 (Ⅱ)
(Ⅱ)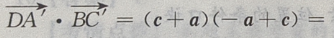
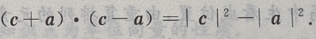 (Ⅲ)
(Ⅲ)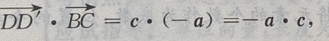 由已知,a,c是正四棱柱的棱,a,b,c两两垂直
由已知,a,c是正四棱柱的棱,a,b,c两两垂直

2、已知设△ABC的三边长为a、b、C,2sin2A=3(sin2B+sin2C)且cos2A+3cosA+3cos(B-C)=1,求证:a:b:c= :1:1。
:1:1。
答 案:因所证的是△ABC三边的比,所以可将题中角的关系式转化为边的关系式,需用正弦定理关于题中的余弦关系式可通过恒等变形化为正弦函数的关系式。 ∵2sin2A=3(sin2B+sin2C)…① 由正弦定理得,2a2=3(b2+c2)…②
∵cos2A+3cosA+3cos(B-C)=1
∴3[cosA+cos(B-C)]=1-cos2A.
∵A=180°-(B+C)
∴3[-cos(B+C)+cos(B-C)]=2sin2A.
由两角和与差的余弦公式得
6sinBsinB=2sin2A…③
由①③得,2sinBsinC=sin2B+sin2C.
sin2B-2sinBsinC+sin2C=0
(sinB-sinC)2=0
sinB= sinC.
由正弦定理得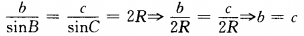
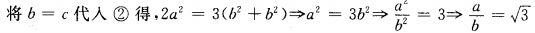
∴a:b=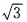 :1
:1
于是a:b:c=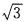 :1:1。
:1:1。
3、已知log53=a,log54=b,求log2512关于a,b的表达式。
答 案: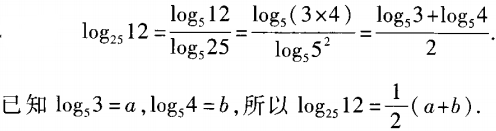
4、已知函数f(x)=(x-4)(x2-a) (I)求f"(x); (Ⅱ)若f"(-1)=8,求f(x)在区间[0,4]的最大值与最小值
答 案: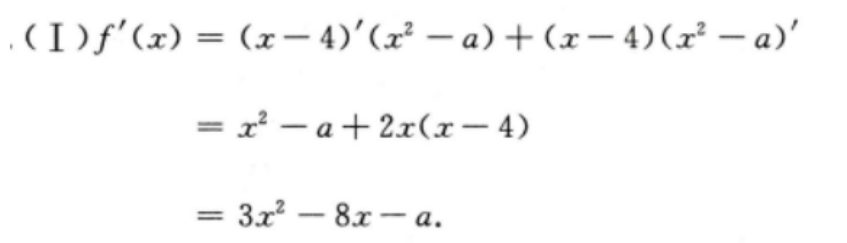

填空题
1、已知△ABC的面积为64,且c与b的等比中项为12,则sinA=______。
答 案:
解 析: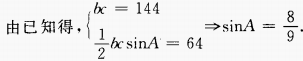
2、已知A(0,1),B(1,2),存在一点P是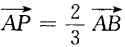 ,则点P的坐标是______。
,则点P的坐标是______。
答 案: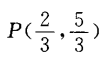
解 析: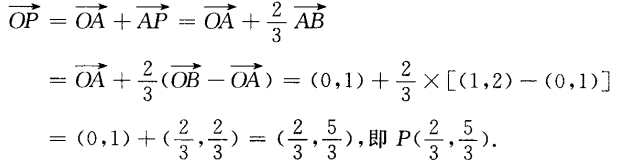
精彩评论