2025年成考高起点每日一练《数学(理)》3月25日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、曲线y=x+2在点（1，2）处的切线斜率为（）。

• A：1
• B：2
• C：-1
• D：4

答 案：A

解 析：方法一：∵y=x+2，k=y’＝1 方法二：也可用直线方程y=kx+b直接得出k=1。  

2、过点P(2,3)且在两轴上截距相等的直线方程为()  

• A：
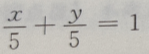
• B：
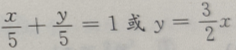
• C：x+y=5
• D：

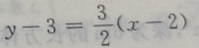
答 案：B

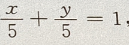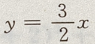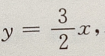解 析：选项A中，在x、y 轴上截距为 5.但答案不完整 所以选项B中有两个方程，在x轴上横截距与y轴上的纵截距都为0，也是相等的 选项C,虽然过点(2,3),实质上与选项A相同.选项 D,转化为:答案不完整  

3、（）。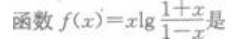  

• A：奇函数
• B：偶函数
• C：非奇非偶函数
• D：无法判断

答 案：B

解 析：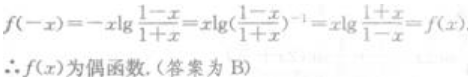

4、已知a=（-1，3），b=（-2，3），c=（0，-1），则（a·b）·c=（）。

• A：（0，-11）
• B：（11，-1）
• C：10
• D：-10

答 案：A

解 析：（a·b）·c=（-1,3）·（-2.3）·（0.-1）=（2+9）·（0，-1）=11×（0，-1）=（0，-11），故应选A。 注:向量的和、差，数乘向量结果仍为向量，向量的积为数量，掌握这些结果在解选择题时可直接用排除法，会加快解题的速度以及提高解题的准确率。

主观题

1、设函数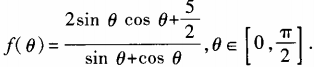（1）求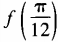；（2）求函数f（θ）最小值。

答 案：

2、在△ABC中，B=120°,BC=4,△ABC的面积为，求AC.

答 案：由△ABC的面积为得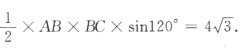所以AB =4.因此所以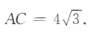

3、已知a^m=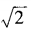，an=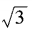，求a3^n-4m的值。  

答 案：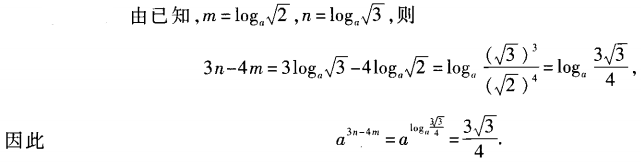

4、如图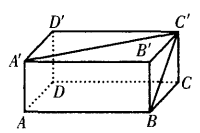，已知长方体的长和宽都是4cm，高是2cm。求 （1）BC和A’C’所成的角是多少度?
（2）A’B’和DD’的距离是多少?

答 案：（1）在长方体中BC和A’C’不在同一个平面内 所以BC和A’C’是异面直线 ∵在长方体中BC//B’C’ ∴∠A’C’B’是异面直线BC和A’C’所成的角
∵A’C’B’=45°
异面直线BC和A’C’所成的角是45°
（2）A’B’和DD’是异面直线
∵A’D’⊥A’B’ A’D’⊥DD’
∴A’D’的长即为异面直线A’B’和DD’的距离
∵A’D’=4
∴A’B’和DD’间的距离为4cm。

填空题

1、与已知直线 7x+24y-5 =0 平行，且距离等于3的直线方程是______。  

答 案：7x+24y+70=0或7z+24y-80-0

解 析：

2、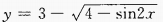的值域是______。  

答 案：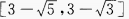

解 析：当sin2x=-1时，y最小值当 sin2x=1时,