2025年成考高起点每日一练《数学(文史)》3月18日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、设甲：四边形ABCD是平行四边形，乙：四边形ABCD是正方形，则（）。

• A：甲是乙的充分条件，但不是乙的必要条件
• B：甲是乙的必要条件，但不是乙的充分条件
• C：甲是乙的充分必要条件
• D：甲不是乙的充分条件，也不是乙的必要条件

答 案：B

2、从13名学生中选出2人担任正副班长，不同的选举结果共有（）。

• A：26
• B：78
• C：156
• D：169

答 案：C

3、已知两数的等差中项为10，等比中项为8，则以这两数为根的一元二次方程是（）。

• A：x²+10x+8=0
• B：x²-10x+64=0
• C：x²-20x+8=0
• D：x²-20x+64=0

答 案：D

4、若函数y=f（z）在[a，b]上单调，则使得y=f（x+3）必为单调函数的区间是（）。

• A：[a，b+3]
• B：[a+3，b+3]
• C：[a-3，b-3]
• D：[a+3，b]

答 案：C

主观题

1、已知a,b,c成等比数列，x是a，b的等差中项，y是b，c的等差中项证明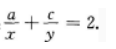  

答 案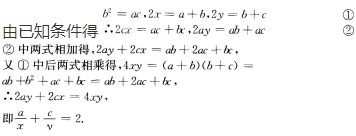： 考点 本题考查考生对等差中项和等比中项公式的理解及运用．

2、已知函数f（x）=2x³-3x²，求
（1）函数的单调区间；

（2）函数f（x）在区间[-3，2]的最大值与最小值。

答 案：

3、如图9-4，已知测速站P到公路L的距离为40米，一辆汽车在公路L上行驶，测得此车从A点行驶到8点所用的时间为2秒，并测得∠APO=60°，∠BPO=30°，计算此车从A到B的平均速度为多少km/h（结果保留到个位），并判断此车是否超过了80km/h的限制速度。

答 案：此车从A到B的平均速度为83（km/h），已经超过80km/h的限制速度。

4、等差数列{an}的通项公式为an=3n-1，在{an}中，每相邻的两项之间插人三项，构成新的等差数列{bn}． (Ⅰ)求{bn}的通项公式； (Ⅱ)求{bn}前10项的和．

答 案： 考点本题主要考查等差数列的通项公式和前n项和公式的运用，是成人高考常见题型．

填空题

1、任选一个不大于20的正整数,它恰好是3的整数倍的概率是（）  

答 案：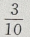

解 析：设n为不大于20的正整数的个数,则n=20,m为在这20个数中3的倍数:3,6、9、12、15、18的个数。 ∴m=6，∴所求概率=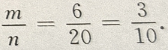  

2、log₂[log₂（log₃81）]=______。  

答 案：1

解 析：由于log₃81=log₃3⁴=4，于是 原式=log₂（log₂4）=log₂2=1。