2025年成考高起点每日一练《数学(理)》3月12日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、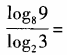 ()。
()。
- A:1
- B:2
- C:
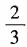
- D:
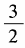
答 案:C
解 析:由于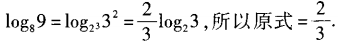
2、设甲:二次不等式x2+px+q>0的解集为空集合;乙:△=p2-4q<0则()。
- A:甲是乙的必要条件,但不是乙的充分条件
- B:甲是乙的充分条件,但不是乙的必要条件
- C:甲不是乙的充分条件,也不是乙的必要条件
- D:甲是乙的充分必要条件
答 案:D
解 析:由于二次不等式x2+px+q>0的解集为空集合△=p2-4q<0,则甲是乙的充分必要条件(答案为 D)
3、下列各式中正确是()。
- A:
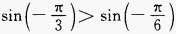
- B:
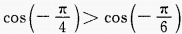
- C:
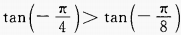
- D:
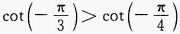
答 案:D
解 析: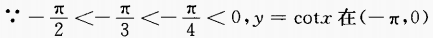 上为减函数,故
上为减函数,故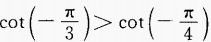
4、下列函数中为奇函数的是()。
- A:y=2lgx
- B:y=3x+3-x
- C:y=x3+sin2x
- D:y=x3+tanx
答 案:D
解 析:对于D,f(-x)=(-x)3+tan(-x)=-(x3+tanx)=-f(x)。答案为D。
主观题
1、在正四棱柱ABCD-A'B'C'D'中, (Ⅰ)写出向量
(Ⅰ)写出向量 和
和 关于基底{a,b,c}的分解式;
(Ⅱ)求证:
关于基底{a,b,c}的分解式;
(Ⅱ)求证: (Ⅲ)求证:
(Ⅲ)求证:
答 案:(Ⅰ)由题意知(如图所示) 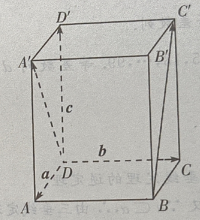
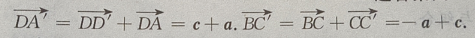
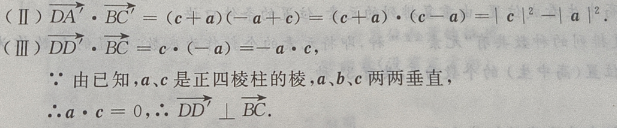
2、已知抛物线C:y2=2px(p>0)的焦点到准线的距离为1。 (I)求C的方程; (Ⅱ)若A(1,m)(m>0)为C上一点,O为坐标原点,求C上另一点B的坐标,使得OA⊥OB
答 案:(I)由题意,该抛物线的焦点到准线的距离为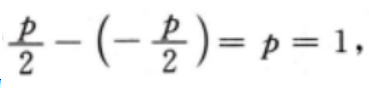 所以抛物线C的方程为
所以抛物线C的方程为 (Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得
(Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得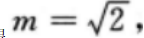 因此A点坐标为
因此A点坐标为 设B点坐标为
设B点坐标为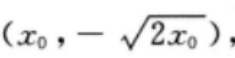 则
则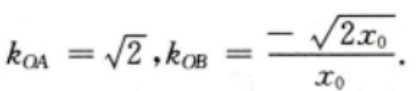 因为
因为 则有
则有 即
即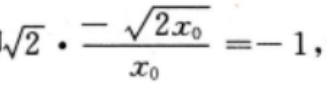 解得x0=4
所以B点的坐标为
解得x0=4
所以B点的坐标为
3、已知数列{an}中,a1=2,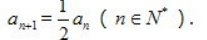 (Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}前5项的和 S5
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}前5项的和 S5
答 案:解:
4、记△ABC的内角A,B,C的对边分别为a,b,c,已知B=60°,b2=ac,求A。
答 案:由余弦定理b2=a2+c2-2accosB,可得ac=a2+c2-ac,即a2+c2-2ac=(a-c)2=0,解得a=c。 又因为B=60°,故△ABC为等边三角形,所以A=60°
填空题
1、若tanα-cotα=1,则 =______。
=______。
答 案:4
解 析:由立方差公式得,tan3α-cot3α=(tana-cotα)(tan2α+tanαcota+cot2α)(tana-cotα)[(tanα-cotα)2+3tanαcotα]=4
2、已知角α的终边过点P(-8m,-6cos60°)且cosα=-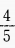 ,则m______。
,则m______。
答 案: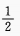
解 析:∵P(-8m,-3)且cosα= ∴P点在第三象限
∴m>0∵y=-3,r=5∴x=-8m=-4
∴P点在第三象限
∴m>0∵y=-3,r=5∴x=-8m=-4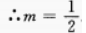
精彩评论