2025年成考专升本每日一练《高等数学一》3月12日专为备考2025年高等数学一考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、若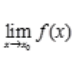 存在,
存在,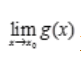 不存在,则()。
不存在,则()。
- A:
 与
与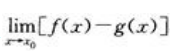 都不存在
都不存在 - B:
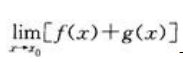 与
与 都存在
都存在 - C:
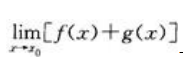 与
与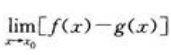 之中的一个存在
之中的一个存在 - D:
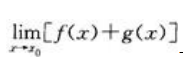 存在与否与f(x),g(x)的具体形式有关
存在与否与f(x),g(x)的具体形式有关
答 案:A
解 析:根据极限的四则运算法则可知: ,
,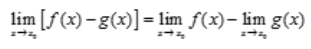 ,所以当
,所以当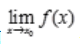 存在,
存在,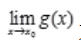 不存在时,
不存在时,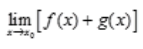 ,
,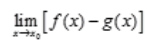 均不存在。
均不存在。
2、微分方程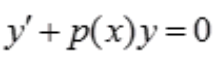 的通解为()。
的通解为()。
- A:

- B:y=

- C:y=
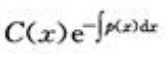
- D:y=
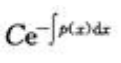
答 案:D
解 析:由一阶线性微分方程的通解公式可知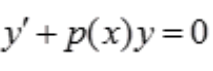 的通解为
的通解为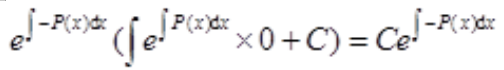
3、设区域D为x2+y2≤4,则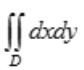 =()。
=()。
- A:4π
- B:3π
- C:2π
- D:π
答 案:A
解 析:由二重积分的性质可知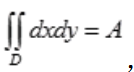 A为区域D的面积.由于D为x2+y2≤4表示圆域,半径为2,A=π×22=4π。
A为区域D的面积.由于D为x2+y2≤4表示圆域,半径为2,A=π×22=4π。
主观题
1、计算极限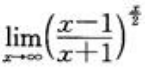 .
.
答 案:解:原式=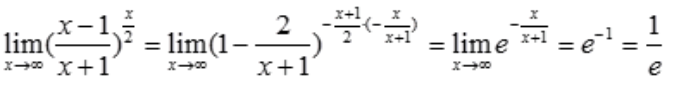
2、求微分方程 的通解.
的通解.
答 案:解:对应齐次微分方程的特征方程为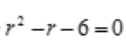 ,解得r1=3,r2=-2.所以齐次通解为
,解得r1=3,r2=-2.所以齐次通解为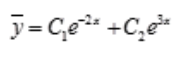 。设方程的特解设为y*=(Ax+B)ex,代入原微分方程可解得,A=
。设方程的特解设为y*=(Ax+B)ex,代入原微分方程可解得,A=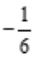 ,B=
,B=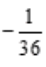 .即非齐次微分方程特解为
.即非齐次微分方程特解为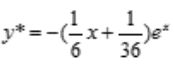 。所以微分方程
。所以微分方程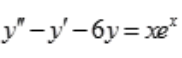 的通解为
的通解为 。
。
3、将函数f(x)=sinx展开为 的幂级数.
的幂级数.
答 案:解:由于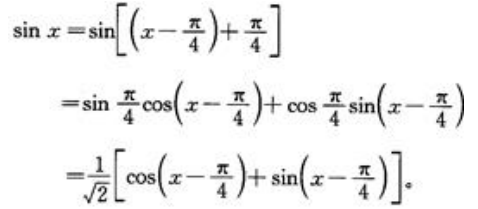 若将
若将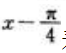 看成整体作为一个新变量,则套用正、余弦函数的展开式可得
看成整体作为一个新变量,则套用正、余弦函数的展开式可得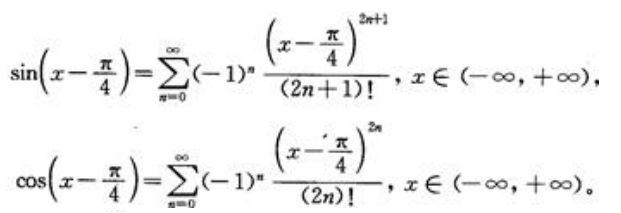 从而有
从而有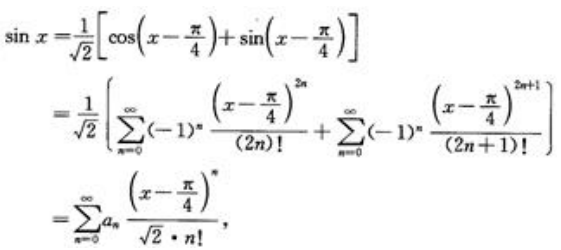 其中
其中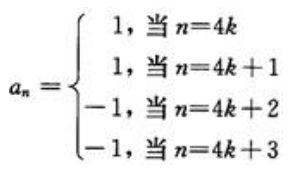 (k为非负整数)。
(k为非负整数)。
填空题
1、曲线y=x2-x在点(1,0)处的切线斜率为()。
答 案:1
解 析:点(1,0)在曲线y=x2-x上,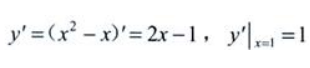 ,故点(1,0)处切线的斜率为1。
,故点(1,0)处切线的斜率为1。
2、设y=sin(x+2),则y'=()。
答 案:cos(x+2)
解 析: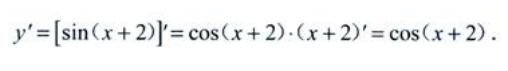
3、设函数z=xy,则全微分dz_______.
答 案: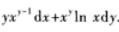
解 析: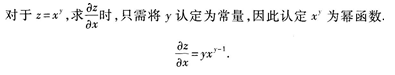

简答题
1、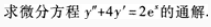
答 案:

精彩评论