2025年成考高起点每日一练《数学(文史)》3月11日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、甲坛有8个小球，乙坛有4个小球，所有小球颜色各不相同，现从甲坛中取2个小球，乙坛中取1个小球，则取出3个球的不同取法共有（）。

• A：224种
• B：112种
• C：32种
• D：1320种

答 案：B

解 析：C8（2）×C4（1）=112（种）。  

2、函数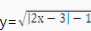的定义域是（）。

• A：{x｜z∈R且x≠}
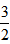• B：{x｜x≥｝
• C：{x｜x≥2}
• D：{x｜x≥2或x≤1｝

答 案：D

3、（）。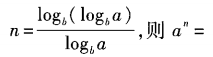

• A：1
• B：b
• C：log_ab
• D：log_ba

答 案：D

解 析：由已知，nlog_ba=log_b（log_ba），log_baⁿ=log_b（log_ba）， 所以aⁿ=log_ba。  

4、已知集合A={0，1，2，3，4}，B={x|0＜x＜4}，则A∩B=（）。  

• A：{0，1，2，3}
• B：{1，2，3}
• C：{1，2}
• D：{0，4}

答 案：B

主观题

1、求下列函数的最大值、最小值和最小正周期： （1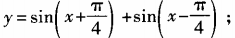） 2）y=6cosx+8sinx

答 案： 所以函数的最大值是最小值是最小正周期为2π， （2）要将6cosx+8sinx化为sinαcosx+cosαsinx这种形式，需使cosx与sinx的系数平方和为1，为此，将已知函数化为 因此,函数的最大值是10,最小值是-10,最小正周期为2π

2、如图9-4，已知测速站P到公路L的距离为40米，一辆汽车在公路L上行驶，测得此车从A点行驶到8点所用的时间为2秒，并测得∠APO=60°，∠BPO=30°，计算此车从A到B的平均速度为多少km/h（结果保留到个位），并判断此车是否超过了80km/h的限制速度。

答 案：此车从A到B的平均速度为83（km/h），已经超过80km/h的限制速度。

3、已知等差数列前n项和 （Ⅰ）求通项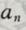的表达式 （Ⅱ）求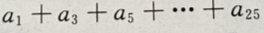的值  

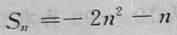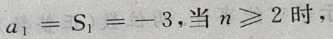
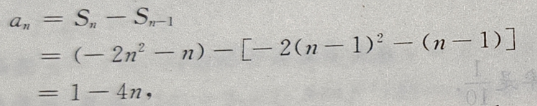
答 案：（Ⅰ）当n=1时，由得 也满足上式，故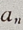=1-4n（n≥1） （Ⅱ）由于数列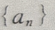是首项为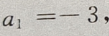公差为d=-4的等差数列，所以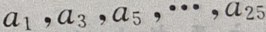是首项为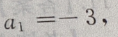公差为d=-8，项数为13的等差数列，于是由等差数列前n项和公式得：  

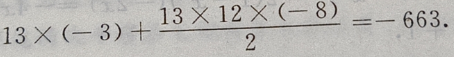
4、已知log₅3=a，log₅4=b，求log₂₅12关于a，b的表达式。  

答 案：

填空题

1、袋中装有3个白球，2个红球，从中任取2个球，取到2个都是红球的概率是______。  

答 案：

解 析：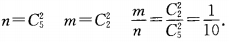

2、已知向量a=(3,2),b=(-4,x),且a⊥b，则x=（）  

答 案：6

解 析：∵a⊥b， ∴3×(-4)+2x=0 ∴x=6.