2025年成考高起点每日一练《数学(理)》3月11日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、已知a,b为任意正实数,则下列等式中恒成立的是()。
- A:ab=ba
- B:2a+b=2a+2b
- C:
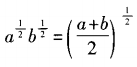
- D:algb=blga
答 案:D
解 析:由于a,b为任意正实数,不妨取a=1,b=2。在A项中,12≠21;B项中,21+2≠21+22;C项中,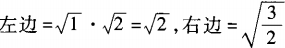 ,而
,而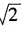 ≠
≠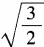 。故选D。
。故选D。
2、在△ABC中,已知2B= A+C, = ac,则B-A=()
= ac,则B-A=()
- A:0
- B:
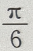
- C:
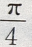
- D:
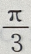
答 案:A
解 析:在△ABC中,A+B+C=π,A+C=π-B,① 因为2B=A+C,②
由①②得2B=π-B,
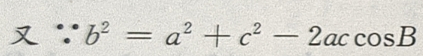
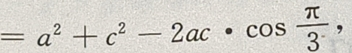
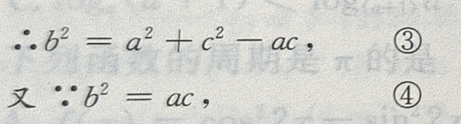 由③④得
由③④得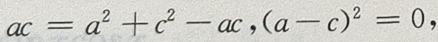 a=c。所以A=C,又
a=c。所以A=C,又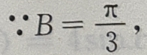 所以△ABC为等边三角形,则B-A=0
所以△ABC为等边三角形,则B-A=0
3、与1775°的终边相同的绝对值最小的角是()。
- A:335°
- B:-25°
- C:25°
- D:155°
答 案:B
解 析:1775°=5×360°+(-25°),故所求角为-25°。
4、某车间有甲、乙两台机床,已知甲机床停机与不停机的概率为0.06,乙机床停机的概率为0.07,甲、乙两车床同时停机的概率是()。
- A:0.13
- B:0.0042
- C:0.03
- D:0.04
答 案:B
解 析:本题的事件可以认为甲机床停机与不停机并不影响乙机床停机的概率,所以此题由实际问题判断属于相互独立同时发生事件,可用乘法公式求其概率为0.06×0.07=0.0042。
主观题
1、设A1A2A3A4A5A6为正六边形,如图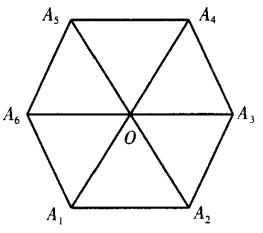 ,O为它的中心。 (1)求证:
,O为它的中心。 (1)求证: 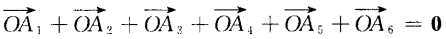 (2)
(2)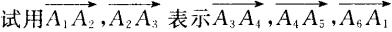
答 案:已知A1A2A3A4A5A6 为正六边形,即|A1A2|=|A3A4|=......|A6A1|.要证6个向量的和为0.只需证其中3个向量与另3个向量的长度相等、方向相反即可.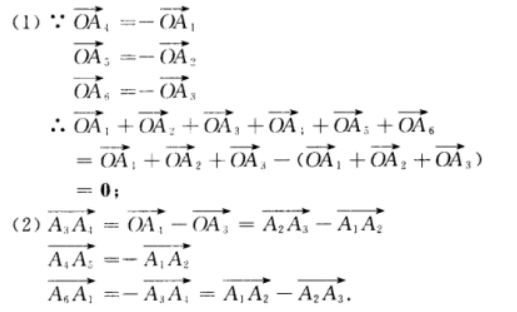
2、计算。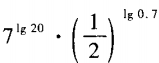
答 案: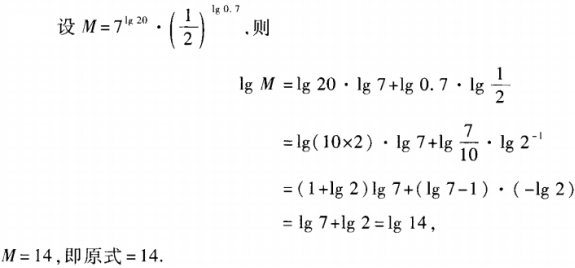
3、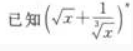 展开式的二项式系数之和比
展开式的二项式系数之和比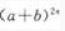 展开式的二项式系数之和小240。 求:(1)
展开式的二项式系数之和小240。 求:(1)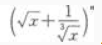 展开式的第3项;
展开式的第3项;
(2)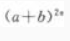 展开式的中间项。
展开式的中间项。
答 案:
4、某气象预报站天气预报的准确率为80%,计算(1)5次预报中恰有4次准确的概率; (2)5次中至少有次准确的概率.(计算结果保留两个有效数字).
答 案: 把每次预报看做一次试验,“预报结果准确”看成事件P(A)=0.8,本题就相当于在5次独立重复试验中求A恰好发生4次(或至少4次)的概率,此题属于独立重复试验,由公式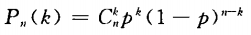 来求解。 (1)n=5;p=0.8;k=4
来求解。 (1)n=5;p=0.8;k=4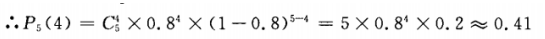 即恰有4次准确的概率为0.41.
(2)5次至少有4次准确的概率,就是5次中恰有4次准确的概率与5次预报中都准确的概率的和,即
即恰有4次准确的概率为0.41.
(2)5次至少有4次准确的概率,就是5次中恰有4次准确的概率与5次预报中都准确的概率的和,即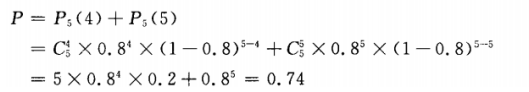 即至少有4次准确的概率为0.74。
即至少有4次准确的概率为0.74。
填空题
1、lg(tan43°tan45°tan47°)=()
答 案:0
解 析:lg(tan43°tan45°tan47°)=lg(tan43°tan45°cot43°)=lgtan45°=lg1=0
2、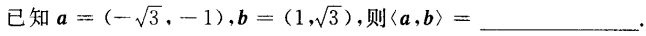
答 案:;150°
解 析: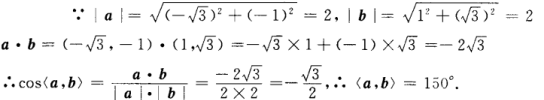
精彩评论