2025年成考高起点每日一练《数学(理)》3月10日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、过直线3x+2y+1=0与2x-3y+5=0的交点,且垂直于直线L:6x-2y+5=0的直线方程是()。
- A:x-3y-2=0
- B:x+3y-2=0
- C:x-3y+2=0
- D:x+3y+2=0
答 案:B
解 析: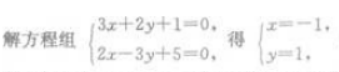 即两直线的交点坐标为(-1,1)
又直线L:6x-2y+5=0的斜率为3 ,则所求的直线方程为
即两直线的交点坐标为(-1,1)
又直线L:6x-2y+5=0的斜率为3 ,则所求的直线方程为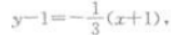 即x+3y-2=0.
即x+3y-2=0.
2、设F1和F2为双曲线的两焦点,点P在双曲线上,则||PF2|-|PF2||=()。
- A:4
- B:2
- C:1
- D:
答 案:A
解 析:由题意有a2=4.a=2,由双曲线的定义,可知||PF2|-|PF2||=2a=4.(答案为A)
3、设log2x=a,则log2(2x2)=()。
- A:2a2+1
- B:2a2-1
- C:2a-1
- D:2a+1
答 案:D
解 析:本题主要考查的知识点为对数函数的性质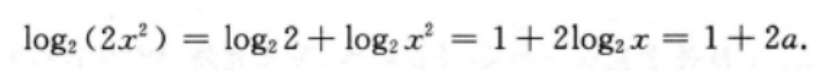
4、已知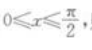 则函数 y=sinx+cosx的值城为()。
则函数 y=sinx+cosx的值城为()。
- A:[-1,1]
- B:
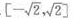
- C:
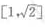
- D:
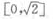
答 案:C
主观题
1、设函数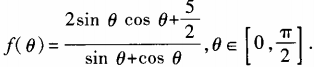 (1)求
(1)求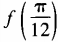 ;(2)求函数f(θ)最小值。
;(2)求函数f(θ)最小值。
答 案:
2、空间有四个点,如果其中任何三点不在同一直线上,可以确定几个平面?
答 案:根据公理,在所给定的四点中任取三点,可确定一个平面,由组合公式 所以共可确定四个平面。
所以共可确定四个平面。
解 析:空间有n个点,如果其中任何三点不在同一直线上,可以确定 个平面。
个平面。
3、已知lg2=a,lg3=b,求lg0.15关于a,b的表达式。
答 案: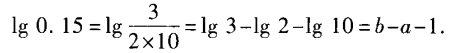
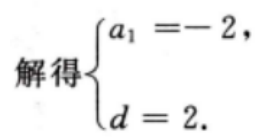
4、已知等差数列{an}中,a1+a2+a3=6,a2+a4+a5= 12求{an}的首项与公差。
答 案:因为{an}为等差数列,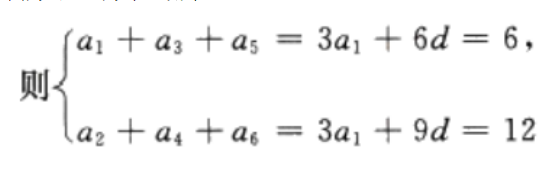
填空题
1、过点(2,0)作圆x2+y2=1的切线,切点的横坐标为()。
答 案: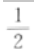
解 析:本题主要考查的知识点为圆的切线.
设切点(x0,y0)则有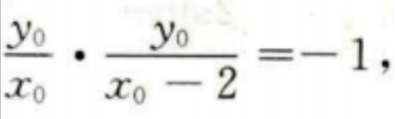 即
即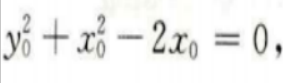
 所以
所以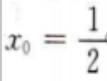 故切点横坐标为
故切点横坐标为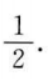
2、不等式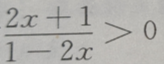 的解集为()
的解集为()
答 案: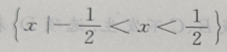
解 析:

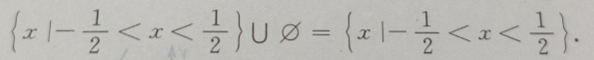
精彩评论