2025年成考高起点每日一练《数学(文史)》3月7日专为备考2025年数学(文史)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、盒中有20节电池,其中有2节是废品,现从中取3节,其中至少有一节废品的概率是()。
- A:
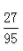
- B:
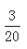
- C:
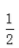
- D:
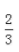
答 案:A
2、已知x+x-1=2cos40°,则x4+x-4=()。
- A:2cos20°
- B:-2cos20°
- C:2sin80°
- D:-2sin80°
答 案:B
解 析:由已知得(x+x-1)2=(2 cos 40°)2,x2+2+x-2=4cos240° x2+x-2=2(2 cos240°-1)= 2cos 80°同样可得x4+x-4=2 cos 160°=-2 cos 20°故选B。
3、一批产品共有5件,其中4件为正品,1件为次品,从中一次取出2件均为正品的概率为()。
- A:0.6
- B:0.5
- C:0.4
- D:0.3
答 案:A
解 析:本题主要考查的知识点为随机事件的概率。 一次取出2件均为正品的概率为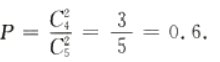
4、函数f(x)=(x2-2)3+4的极小值为()。
- A:f(
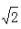 )
) - B:f(-
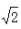 )
) - C:f(0)
- D:f(4)
答 案:C
主观题
1、设椭圆的中心是坐标原点,长轴在x轴上,离心率 已知点P
已知点P 到圆上的点的最远距离是
到圆上的点的最远距离是 求椭圆的方程
求椭圆的方程
答 案:由题意,设椭圆方程为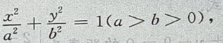 由
由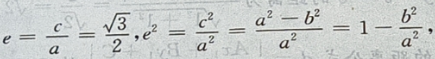
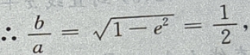 设P
设P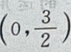 点到椭圆上任一点的距离为 d,
点到椭圆上任一点的距离为 d,
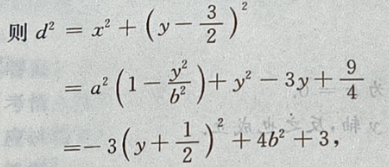
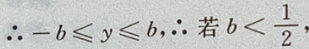 则在y=-b时,
则在y=-b时,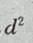 最大,即d也最大。
最大,即d也最大。
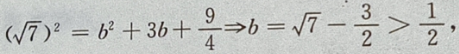

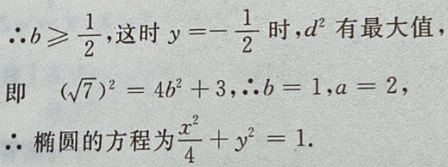
2、求下列函数的最大值、最小值和最小正周期: (1)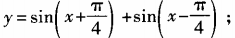 2)y=6cosx+8sinx
2)y=6cosx+8sinx
答 案: 所以函数的最大值是
所以函数的最大值是 最小值是
最小值是 最小正周期为2π,
(2)要将6cosx+8sinx化为sinαcosx+cosαsinx这种形式,需使cosx与sinx的系数平方和为1,为此,将已知函数化为
最小正周期为2π,
(2)要将6cosx+8sinx化为sinαcosx+cosαsinx这种形式,需使cosx与sinx的系数平方和为1,为此,将已知函数化为 因此,函数的最大值是10,最小值是-10,最小正周期为2π
因此,函数的最大值是10,最小值是-10,最小正周期为2π
3、设椭圆的中心是坐标原点,长袖在x轴上,离心率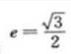 ,已知点P(0,3/2)到椭圆上的点的最远距离是
,已知点P(0,3/2)到椭圆上的点的最远距离是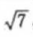 ,求椭圆的方程。
,求椭圆的方程。
答 案:
4、设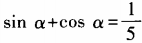 (0<α<π),求tanα的值。
(0<α<π),求tanα的值。
答 案:
填空题
1、点(4,5)关于直线y=x的对称点的坐标为()
答 案:(5,4)
解 析:点(4,5)关于直线y=x的对称点为(5,4).
2、101-lg2=______。
答 案:5
解 析: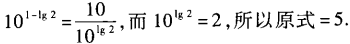
精彩评论