2025年成考高起点每日一练《数学(理)》3月7日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、设集合M={x||x-2|<1},N={x|x>2},则M∩N=()
- A:{x|1<x<3}
- B:{x|x>2}
- C:{x|2<x<3}
- D:{x|1<x<2}
答 案:C
解 析:M={x||x-2|<1}解得{x|-1<x-2<1}={x|1<x<3},故M∩N={x|2<x<3}
2、设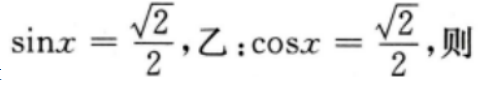 ()
()
- A:甲是乙的充分条件但不是必要条件
- B:甲是乙的必要条件但不是充分条件
- C:甲是乙的充要条件
- D:甲既不是乙的充分条件也不是乙的必要条件
答 案:D
解 析:本题主要考查的知识点为简易逻辑 由于 故甲既不是乙的充分条件,也不是乙的必要条件
故甲既不是乙的充分条件,也不是乙的必要条件
3、把一对骰子掷一次,得到11点的概率是()。
- A:
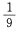
- B:
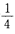
- C:
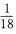
- D:
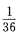
答 案:C
解 析:本题的试验是掷一对骰子,若把第一颗骰子掷出的点数写在前面,第二颗点数写在后 面,试验的等可能结果共有【(1,1),(1,2),(1,3)(1,4),(1,5),(1,6),(2,1),…,(5,6),(6,1),…,(6,5),(6,6)】36种,此题属于等可能事件的概率n=36,m=2,其概率为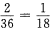 ,故选C。
,故选C。
4、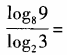 ()。
()。
- A:1
- B:2
- C:
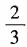
- D:
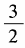
答 案:C
解 析:由于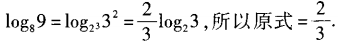
主观题
1、已知am=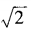 ,an=
,an=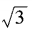 ,求a3n-4m的值。
,求a3n-4m的值。
答 案: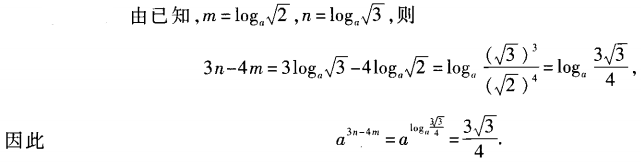
2、已知数列{an}中,a1=2,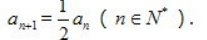 (Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}前5项的和 S5
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}前5项的和 S5
答 案:解:
3、计算 (1)tan5°+ cot5°- 2sec80°
(2)tan15°+cot15
(3)sin15°sin75°
答 案:(1)化切割为弦进行运算。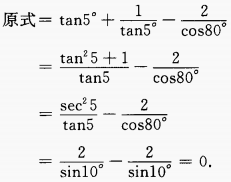 (2)
(2) 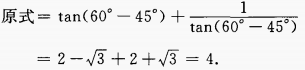 (3)
(3) 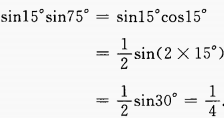
4、记△ABC的内角A,B,C的对边分别为a,b,c,已知B=60°,b2=ac,求A。
答 案:由余弦定理b2=a2+c2-2accosB,可得ac=a2+c2-ac,即a2+c2-2ac=(a-c)2=0,解得a=c。 又因为B=60°,故△ABC为等边三角形,所以A=60°
填空题
1、点B(4,-5)按向量a平移后的对应点B0(-4,7),则a的坐标是______。
答 案:(-8,12)
解 析:由平移公式得-4=4+a1,7=-5+a2→a1=-8,a2=12 ∴a的坐标是(-8,12)。
2、在自然数1、2、…、100中任取一个数,该数能被3整除的概率是______。
答 案:0.33
解 析:此题随机试验包含的基本事件总数n=100,且每个数能被取到的机会均等,即属于等可能事件的概率能被3整除的自然数的个数m=33,故所求概率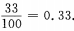
精彩评论