2025年成考高起点每日一练《数学(文史)》3月5日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、设f（x）=x³+4x²+11x+7，则f（x+1）=（）。

• A：x³+7x²+22x+23
• B：x³—7x²+22x+23
• C：x³+7x²-22x+23
• D：x³-7x²-22x+23

答 案：A

解 析：f(x+1) =(x+1)³ +4(x+1}²+11(x+1)+7 =x³+3x²+3x+1+4x²+8x+4+11x+11+7 =x³+7x²+22x+23 综上所述，答案:x³+7x²+22x+23

2、设集合P=（1，2，3，4，5），Q={2，4，6，8，10}，则集合P∩Q=（）。  

• A：｛2，4}
• B：｛1，2，3，4，5，6，8，10}
• C：｛2｝
• D：｛4｝

答 案：A

3、已知集合A={0，1，2，3，4}，B={x|0＜x＜4}，则A∩B=（）。  

• A：{0，1，2，3}
• B：{1，2，3}
• C：{1，2}
• D：{0，4}

答 案：B

4、方程36x²-25y²=800的曲线是（）。

• A：椭圆
• B：双曲线
• C：圆
• D：两条直线

答 案：B

解 析：

主观题

1、如图：已知在△ADC中，∠C=90°，∠D=30°，∠ABC=45°，BD=20，求AC(用小数表示，保留一位小数)  

答 案：如图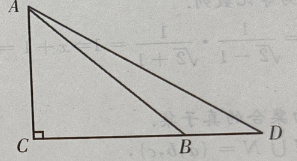  

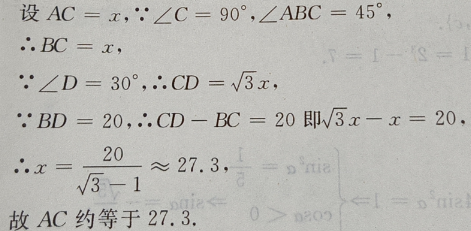
2、cos20°cos40°cos80°的值。  

答 案：

3、已知lg2=a，lg3=b，求lg0.15关于a，b的表达式。  

答 案：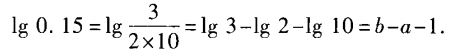

4、（1）已知tanα=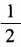 求cot2α的值； （2）已知tan2α=1，求tanα的值。

答 案：（1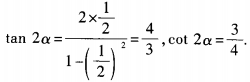） （2）由已知，得 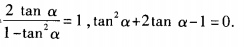解关于tanα的一元二次方程，得tanα=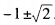

填空题

1、平面内有10个点，任何三点都不在同一直线上，问能连成______条不同的直线。  

答 案：45

2、已知5^a=2，25^b=9，则5^2a-b的值等于______。  

答 案：

解 析：由25^b=9，得5^2b=9，5^b=3。又5^a=2，则