2025年成考高起点每日一练《数学(理)》2月26日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、已知圆的方程为x2+y2-2x+4y+1=0,则圆上一点到直线3x+4y-10=0的最大距离为()。
- A:6
- B:5
- C:4
- D:3
答 案:B
解 析:圆x2+y2-2x+4y+1=0,即(x-1)2+(y+2)2=22的圆心为(1,-2)半径r=2,
圆心(1.-2)到直线3x+4y-10=0的距离是 圆上一点到直线3x+4y-10=0的距离的最大值是3+2=5.(答案为B)
圆上一点到直线3x+4y-10=0的距离的最大值是3+2=5.(答案为B)
2、i为虚数单位,則i•i2•i3•i4•i5的值为()。
- A:1
- B:-1
- C:i
- D:-i
答 案:D
解 析:i•i2•i3•i4•i5=i1+2+3+4+5=i15=-i
3、袋中有6个球,其中4个红球,2个白球,从中随机取出2个球,则其中恰有1个红球的概率为()
- A:

- B:
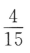
- C:

- D:
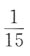
答 案:A
解 析: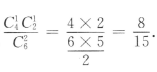
4、过点(-2,2)与直线x+3y-5=0平行的直线是()
- A:x+3y-4=0
- B:3x+y+4=0
- C:x+3y+8=0
- D:3x-y+8=0
答 案:A
解 析:所求直线与x+3y-5=0平行,可设所求直线为x+3y+c=0,将点(一2,2)带入直线方程,故-2+3×2+c=0,解得c=-4,因此所求直线为线为x+3y-4=0.
主观题
1、设 分别讨论x→0及x→1时f(x)的极限是否存在?
分别讨论x→0及x→1时f(x)的极限是否存在?
答 案: ∴f(x)在x=0处极限不存在 同理f(x)在x=1处极限存在
∴f(x)在x=0处极限不存在 同理f(x)在x=1处极限存在
2、已知关于x的二次方程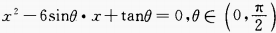 的两根相等,求sinθ+cosθ的值。
的两根相等,求sinθ+cosθ的值。
答 案:

3、建筑一个容积为8000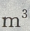 ,深为6m的长方体蓄水池,池壁每
,深为6m的长方体蓄水池,池壁每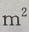 的造价为15元,池底每
的造价为15元,池底每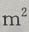 的造价为30元。(I)把总造价y(元)表示为长x(m)的函数;(Ⅱ)求函数的定义域
的造价为30元。(I)把总造价y(元)表示为长x(m)的函数;(Ⅱ)求函数的定义域
答 案: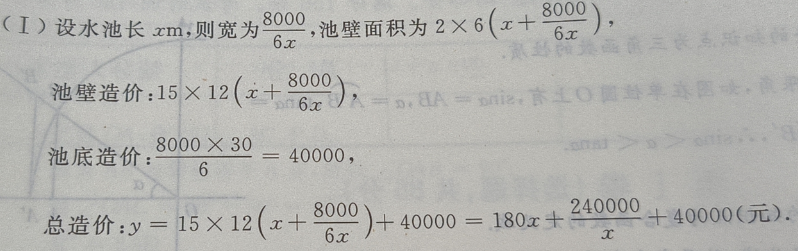

4、已知空间四边形OABC,OB=OC且∠AOB=∠AOC=θ(如图)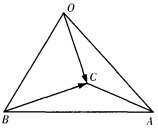 。求证:OA⊥BC。
。求证:OA⊥BC。
答 案:
填空题
1、九个学生期末考试的成绩分别为79 63 88 94 99 77 89 81 85这九个学生成绩的中位数为______。
答 案:85
解 析:本题主要考查的知识点为中位数. 将成绩按由小到大排列:63,77,79,81,85,88,89,94,99.因此中位数为85。
2、函数y=-x2+ax图像的对称轴为x=2,则a=______。
答 案:4
解 析:本题主要考查的知识点为二次函数的性质
由题意,该函数图像的对称轴为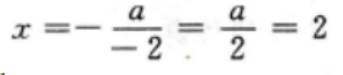
精彩评论