2025年成考高起点每日一练《数学(理)》2月23日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、过点P(2,3)且在两轴上截距相等的直线方程为()
- A:
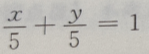
- B:
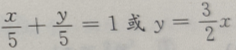
- C:x+y=5
- D:
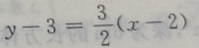
答 案:B
解 析:选项A中,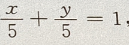 在x、y 轴上截距为 5.但答案不完整 所以选项B中有两个方程,
在x、y 轴上截距为 5.但答案不完整 所以选项B中有两个方程,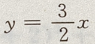 在x轴上横截距与y轴上的纵截距都为0,也是相等的
选项C,虽然过点(2,3),实质上与选项A相同.选项 D,转化为:
在x轴上横截距与y轴上的纵截距都为0,也是相等的
选项C,虽然过点(2,3),实质上与选项A相同.选项 D,转化为: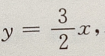 答案不完整
答案不完整
2、已知点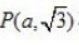 在曲线
在曲线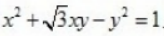 上,那么a的值是()。
上,那么a的值是()。
- A:1
- B:1或-4
- C:-4或-1
- D:-4
答 案:B
3、在单位圆中,弧长为3.2的弧所对的圆心角等于()。
- A:3.2
- B:3.2π
- C:6.4
- D:6.4π
答 案:A
解 析:∵r=1,l=3.2∴a=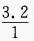 =3.2
=3.2
4、袋中有6个球,其中4个红球,2个白球,从中随机取出2个球,则其中恰有1个红球的概率为()
- A:

- B:
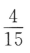
- C:

- D:
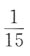
答 案:A
解 析: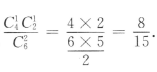
主观题
1、设函数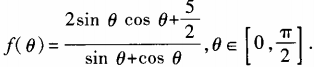 (1)求
(1)求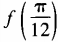 ;(2)求函数f(θ)最小值。
;(2)求函数f(θ)最小值。
答 案:
2、为了测河的宽,在岸边选定两点A和B,望对岸标记物C,测得 AB=120m,求河的宽
AB=120m,求河的宽

答 案:如图,  ∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD=
∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD= =60m,
即河宽为60m
=60m,
即河宽为60m
3、已知等差数列{an}中,a1+a2+a3=6,a2+a4+a5= 12求{an}的首项与公差。
答 案:因为{an}为等差数列,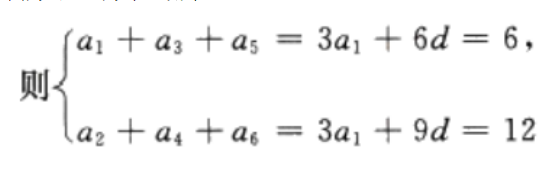
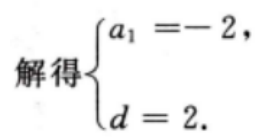
4、求(1+tan10°)(1+tan35°)的值。
答 案:原式=1+tan10°+tan35°+tan10°·tan35°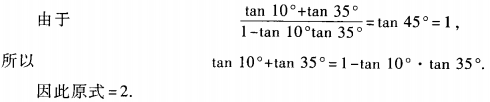
填空题
1、不等式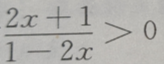 的解集为()
的解集为()
答 案: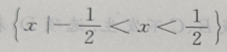
解 析:

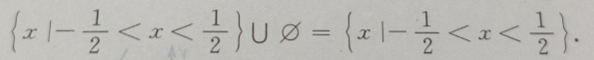
2、在自然数1、2、…、100中任取一个数,该数能被3整除的概率是______。
答 案:0.33
解 析:此题随机试验包含的基本事件总数n=100,且每个数能被取到的机会均等,即属于等可能事件的概率能被3整除的自然数的个数m=33,故所求概率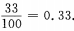
精彩评论