2025年成考高起点每日一练《数学(文史)》2月22日专为备考2025年数学(文史)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、如果点A(1,1)和B(2,4)关于直线y=kx+b对称,则k=()。
- A:-3
- B:
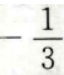
- C:

- D:3
答 案:B
解 析:本题主要考查的知识点为两垂直直线斜率的关系。 直线AB的斜率为: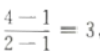 点A、B关于直线y=kx+b对称,因此直线AB与其垂直,故3k=-1,得
点A、B关于直线y=kx+b对称,因此直线AB与其垂直,故3k=-1,得 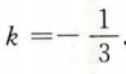
2、已知α为三角形的一个内角,且sinα+cosα=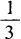 则α∈()。
则α∈()。
- A:
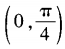
- B:
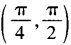
- C:
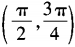
- D:
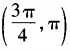
答 案:C
解 析:由已知得 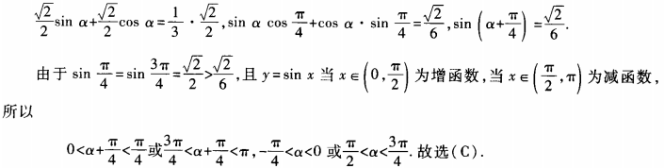
3、不等式x2+x+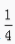 >0的解集是()。
>0的解集是()。
- A:不等于-
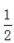 的全体实数
的全体实数
- B:全体实数集
- C:空集
- D:x≠
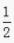 的一切实数
的一切实数
答 案:A
4、若向量a=(1,-1),b=(1,x),且|a+b|=2,则x=()。
- A:-4
- B:-1
- C:1
- D:4
答 案:C
解 析: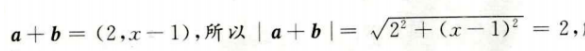 解得x=1 本题主要考查的知识点为向量的加法和模。
解得x=1 本题主要考查的知识点为向量的加法和模。
主观题
1、等差数列{an}的通项公式为an=3n-1,在{an}中,每相邻的两项之间插人三项,构成新的等差数列{bn}. (Ⅰ)求{bn}的通项公式; (Ⅱ)求{bn}前10项的和.
答 案: 考点本题主要考查等差数列的通项公式和前n项和公式的运用,是成人高考常见题型.
考点本题主要考查等差数列的通项公式和前n项和公式的运用,是成人高考常见题型.
2、已知直线l的斜率为1,l过抛物线C: 的焦点,且与C交于A,B两点.
的焦点,且与C交于A,B两点.
(I)求l与C的准线的交点坐标;
(II)求|AB|.
答 案:(I)C的焦点为 ,准线为
,准线为 由题意得l的方程为
由题意得l的方程为 因此l与C的准线的交点坐标为
因此l与C的准线的交点坐标为 (II)由
(II)由 得
得 设A(x1,y1).B(x2,y2),则
设A(x1,y1).B(x2,y2),则 因此
因此
3、已知tan2θ=2tan2ψ+1,求cos2θ+sin2ψ的值。
答 案:由已知,得 
4、教室里有50人在开会,其中学生35人,家长12人,老师3人,现校长在门外听到有人在发言,那么发言人是老师或学生的概率为多少?
答 案:此题属于互斥事件,发言人是老师的概率为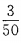 ,是学生的概率为
,是学生的概率为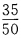 ,故所求概率为。
,故所求概率为。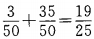
填空题
1、化简sin(x+y)-2cosxsiny=______。
答 案:sin(x-y)
解 析:原式=sinxcosy+cosxsiny-2cosxsiny=sinxcosy-cosxsiny=sin(x-y)
2、101-lg2=______。
答 案:5
解 析: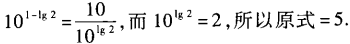
精彩评论