2025年成考高起点每日一练《数学(文史)》2月17日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、已知等比数列a₁=1，a₉=25，则a₅=（）。

• A：25
• B：-5
• C：±5
• D：5

答 案：C

2、已知向量i,j为互相垂直的单位向量，向量a=2i+mj，若|a|=2，则m=（）

• A：-2
• B：-1
• C：0
• D：1

答 案：C

解 析：由题可知a=(2,m),因此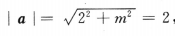，故m=0.

3、函数f(x)=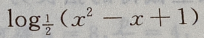的单调增区间是（）

• A：
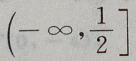
• B：
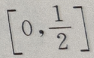
• C：
• D：

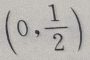
答 案：A

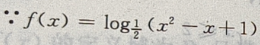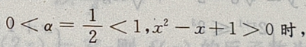
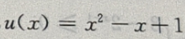解 析：中的的减区间就为f(x)的增区间，设u(x)=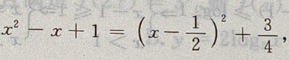当x∈R时，u(x)>0,函数u(x)在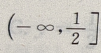是减函数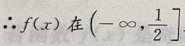， 上是增函数 故f(x)=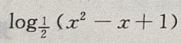的单调增区间为 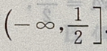ps：关于复合函数的问题要逐步分清每一层次的函数的图像和性质,再结合起来考虑整体,有时也可画出部分函数的图像来帮助分析和理解.  

4、下列函数图象与y=f（x）的图象关于原点对称的是（）。  

• A：y=-f（x）
• B：y=f（-x）
• C：y=-f（-x）
• D：y=｜f（x）｜

答 案：C

主观题

1、已知函数f（x）=（x-4）（x2-a）。（I）求f’（x）；
（Ⅱ）若f’（-1）=8，求f（x）在区间[0，4]的最大值与最小值。

答 案：(I)f'(x) =(x-4)'(x²-a)+(x-4)(x²-a)’ =x²-a+2x(x-4) =3x²-8x-a. (Ⅱ)由于f’(-1)=3+8-a=8,得a=3. 令f'(x)=3x²-8x-3=0,解得x1=3，（舍去）又f（0）=12，f（3）=-6，f（4）=0所以在区间[0，4]上函数最大值为12，最小值为-6

2、已知等差数列前n项和 （Ⅰ）求通项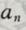的表达式 （Ⅱ）求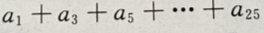的值  

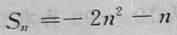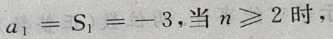
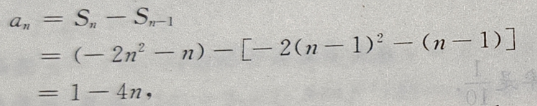
答 案：（Ⅰ）当n=1时，由得 也满足上式，故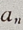=1-4n（n≥1） （Ⅱ）由于数列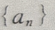是首项为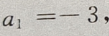公差为d=-4的等差数列，所以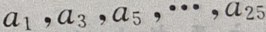是首项为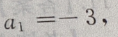公差为d=-8，项数为13的等差数列，于是由等差数列前n项和公式得：  

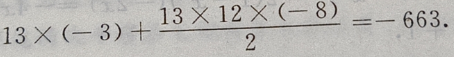
3、已知a^m=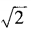，aⁿ=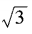，求a^3n-4m的值。  

答 案：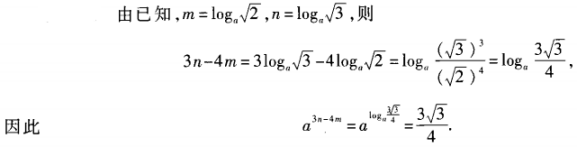

4、等差数列{an}的通项公式为an=3n-1，在{an}中，每相邻的两项之间插人三项，构成新的等差数列{bn}． (Ⅰ)求{bn}的通项公式； (Ⅱ)求{bn}前10项的和．

答 案： 考点本题主要考查等差数列的通项公式和前n项和公式的运用，是成人高考常见题型．

填空题

1、“a=0，且b=0”是“a²+b²=0的”______。  

答 案：充要条件

2、某学科的一次练习中，第一小组5个人成绩如下(单位：分)：98，89，70，92，90，则分数的样本方差为__________．

答 案：88．96

解 析：平均分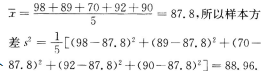 【考点指要】本题主要考查样本的平均数与方差的计算．对于统计问题，只需记清概念和公式，计算时不出错即可．