2025年成考高起点每日一练《数学(文史)》2月15日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、设x，Y为实数，则x²=y²的充分必要条件是（）。

• A：x=Y
• B：x=-y
• C：x³=y³
• D：｜x｜=｜y｜

答 案：D

2、A、B是抛物线y²=8x上两点，且此抛物线的焦点在线段AB上，已知A、B两点的横坐标之和为10，则|AB|=（）。

• A：18
• B：14
• C：12
• D：10

答 案：B

解 析：因为焦点F在AB上,则有FA=A到准线的距离=X1+P/2FB=B到准线的距离=X2+P/2所以,AB=FA+FB=X1+X2+P
又有X1+X2=10.P=4
故有：AB=10+4=14

3、已知tanα，tanβ是方程2x²-4x+1=0的两根，则tan（α+β）=（）。

• A：4
• B：-4
• C：
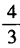
• D：8

答 案：A

解 析：由已知，得tanα+tanβ==2，tanαtanβ=，所以

4、如果方程lg2x+(lg2+lg3)lgx+lg2×lg3=0的两个根分别是x1，x2，那么x1·x2=（　）

• A：lg2×lg3
• B：lg2+lg3
• C：1/6
• D：-6

答 案：C

解 析：【考点指要】本题考查一元二次方程的有关知识及对数的运算法则．注意此方程不是关于2的二次方程，是关于lgx的二次方程，因此运用韦达定理时需要写成lgx1+lgx2与lgx1·lgx2，最好采用题解中换元的方法．

主观题

1、（1）已知tanα=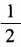 求cot2α的值； （2）已知tan2α=1，求tanα的值。

答 案：（1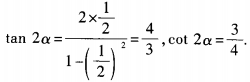） （2）由已知，得 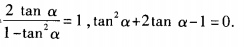解关于tanα的一元二次方程，得tanα=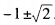

2、设椭圆的中心是坐标原点，长袖在x轴上，离心率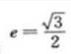，已知点P（0,3/2）到椭圆上的点的最远距离是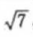，求椭圆的方程。

答 案：

3、已知函数f（x）=2x³-3x²，求
（1）函数的单调区间；

（2）函数f（x）在区间[-3，2]的最大值与最小值。

答 案：

4、求函数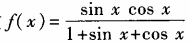（x∈R）的最大值与最小值。  

答 案：设sinx+cosx=t，则（sinx+cosx）²=t²，1+2sinxcosx=t²，sinxcosx= 于是转化为求的最值。 由所设知 上为增函数，故g（t）的最大值为最小值为

填空题

1、在1000000张奖券中，设有1个一等奖，5个二等奖，10个三等奖，从中买一张奖券，中奖的概率是______。  

答 案：

解 析：本题试验属于等可能事件的概率。n=1000000，m=16，所以买一张奖券，中奖的概率

2、已知sin²θ+1=cos²θ，则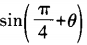的值等于______。  

答 案：

解 析：由已知，cos²θ-sin²θ=1，即cos²θ-（1-cos²θ）=1，cos²θ=1，所以cosθ=±1。 而当cosθ=±1时，sinθ=0。