2025年成考高起点每日一练《数学(理)》2月15日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、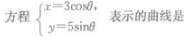 ()。
()。
- A:圆
- B:椭圆
- C:双曲线
- D:抛物线
答 案:B
解 析:消去参数,化曲线的参数方程为普通方程, 
2、函数y=lg(x2-3x+2)的定义域为()。
- A:{x|x<1或x>2}
- B:{x|1<x<2}
- C:{x|x<1}
- D:{x|x>2}
答 案:A
解 析:由x2-3x+2>0,解得x<1或x>2。答案为A。
3、过直线3x+2y+1=0与2x-3y+5=0的交点,且垂直于直线L:6x-2y+5=0的直线方程是()。
- A:x-3y-2=0
- B:x+3y-2=0
- C:x-3y+2=0
- D:x+3y+2=0
答 案:B
解 析: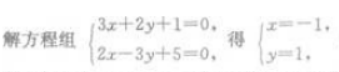 即两直线的交点坐标为(-1,1)
又直线L:6x-2y+5=0的斜率为3 ,则所求的直线方程为
即两直线的交点坐标为(-1,1)
又直线L:6x-2y+5=0的斜率为3 ,则所求的直线方程为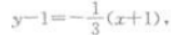 即x+3y-2=0.
即x+3y-2=0.
4、设全集U={0,1,2,3,4},集合M={0,1,2,3,},N={2,3,4},则CuM∩CuN=()。
- A:{2,3)
- B:{0,1,4}
- C:φ
- D:U
答 案:C
解 析:CuM={4},CuN={0,1}.{4}∩{0,1}=∅
主观题
1、已知A(1,4),B(3,8),C(4,10)。求证A、B、C三点共线。
答 案: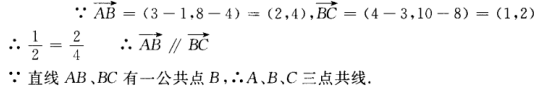
2、已知lg2=a,lg3=b,求lg0.15关于a,b的表达式。
答 案: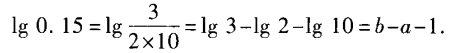
3、已知am=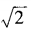 ,an=
,an=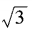 ,求a3n-4m的值。
,求a3n-4m的值。
答 案: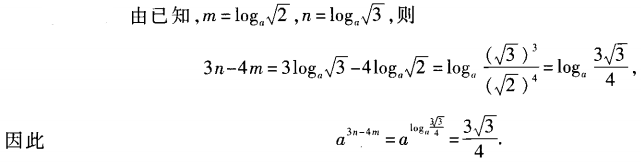
4、已知一组数据9.9;10.3;9.8;10.1;10.4;10;9.8;9.7,计算这组数据的方差。
答 案:
填空题
1、已知角α的终边过点P(-8m,-6cos60°)且cosα=-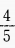 ,则m______。
,则m______。
答 案: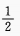
解 析:∵P(-8m,-3)且cosα= ∴P点在第三象限
∴m>0∵y=-3,r=5∴x=-8m=-4
∴P点在第三象限
∴m>0∵y=-3,r=5∴x=-8m=-4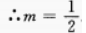
2、函数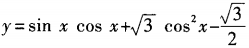 (x∈R)的最小值为______。
(x∈R)的最小值为______。
答 案:-1
解 析: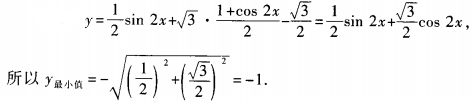
精彩评论