2025年成考高起点每日一练《数学(理)》2月14日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、以椭圆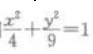 上任一点(长轴两端除外)和两个焦点为顶点的三角形的周长等于()。
上任一点(长轴两端除外)和两个焦点为顶点的三角形的周长等于()。
- A:
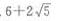
- B:
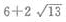
- C:
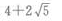
- D:
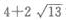
答 案:A
解 析:由椭圆方程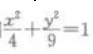 可知a2=9,b2=4,则
可知a2=9,b2=4,则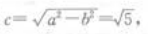 则椭圆上任一点(长轴两端除外)和两个焦点为顶点的三角形的周长等于
则椭圆上任一点(长轴两端除外)和两个焦点为顶点的三角形的周长等于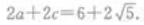
2、函数y=cos4x-sin4x(x∈R)的最小正周期为()。
- A:
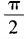
- B:π
- C:2π
- D:4π
答 案:B
解 析:y=(cos2x+sin2x)(cos2x-sin2x)=cos2x, 所以
3、二次函数y=2x2+mx-5在区间(-∞,-1)内是减函数,在区间(-1,+∞)内是增函数,则m的值是()。
- A:4
- B:-4
- C:2
- D:-2
答 案:A
解 析:由题意可知二次函数y=2x2+mx-5的对称轴方程为x=-1,又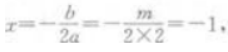 解得m=4
解得m=4
4、已知点M(1,2),N(2,3),则直线MN的斜率为()。
- A:
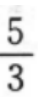
- B:1
- C:
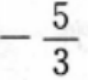
- D:-1
答 案:B
解 析:本题主要考查的知识点为直线的斜率.
直线MN的斜率为: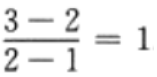
主观题
1、某工厂每月生产x台游戏机的收入为R(x)= +130x-206(百元),成本函数为C(x)=50x+100(百元),当每月生产多少台时,获利润最大?最大利润为多少?
+130x-206(百元),成本函数为C(x)=50x+100(百元),当每月生产多少台时,获利润最大?最大利润为多少?
答 案:利润 =收入-成本, L(x)=R(x)-C(x)= +130x-206-(50x+100)=
+130x-206-(50x+100)=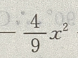 +80x-306
法一:用二次函数
+80x-306
法一:用二次函数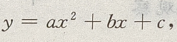 当a<0时有最大值
当a<0时有最大值
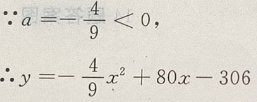 是开口向下的抛物线,有最大值
是开口向下的抛物线,有最大值
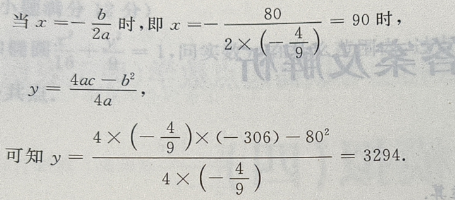 法二:用导数来求解
法二:用导数来求解
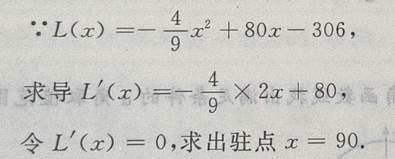 因为x=90是函数在定义域内唯一驻点
所以x=90是函数的极大值点,也是函数的最大值点,其最大值为L(90)=3294
因为x=90是函数在定义域内唯一驻点
所以x=90是函数的极大值点,也是函数的最大值点,其最大值为L(90)=3294
2、当自变量为何值时,函数y=2x3-3x2-12x+21有极值,其极值为多少?
答 案:y'=6x2-6x-12=6(x-2)(x+1) 当x<-1或x>2时,y>0,当-1
3、cos20°cos40°cos80°的值。
答 案:
4、设a为实数,且tanα和tanβ是方程ax2+(2a-3)x+(a-2)=0的两个实根,求tan(α+β)的最小值。
答 案:由已知得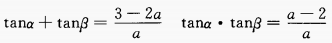

填空题
1、y=cos22x的最大值是______,最小值______,周期T=______。
答 案:1;0;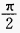
解 析: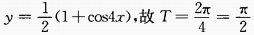 ,最大值为
,最大值为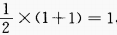 ,最小值为
,最小值为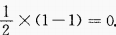
2、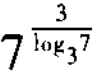 =______。
=______。
答 案:27
解 析: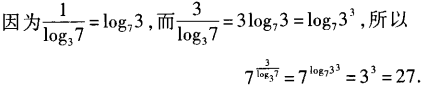
精彩评论