2025年成考高起点每日一练《数学(文史)》2月12日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、设集合M=｛-2，0，2｝，N=｛0｝，则（）。  

• A：N为空集
• B：N∈M
• C：
• D：

答 案：C

解 析：⫋真包含：A真包含于B，则A为B的真子集，例如：若B={1，2}，则A={1}或{2}或空集。因此选C。注意：属于（∈）是元素和集合之间的关系，此题是集合与集合之间关系。

2、一个袋子中装有标号分别为1，2，3，4的四个球，采用有放回的方式从袋中摸球两次，每次摸出一个球，则恰有一次摸出2号球的概率为（）。

• A：
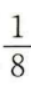
• B：
• C：
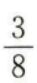
• D：

答 案：C

解 析：本题主要考查的知识点为独立重复试验的概率。 所求概率为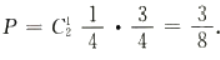

3、设集合A={x|x2-2x-32}，则A∩B=（　）

• A：{x|-1
• B：{x|03}
• C：{x|-3
• D：{x|0

答 案：A

4、若集合M={（x，y）｜3x-2y=-1}，N={（x，y）｜2x+3y=8}，则M∩N=（）。  

• A：（1，2）
• B：{1，2}
• C：{（1，2）}
• D：φ

答 案：C

解 析：M，N都是点集，所以只能选C。  

主观题

1、已知抛物线C：y2=2px（p>0）的焦点到准线的距离为1。（I）求C的方程；
（Ⅱ）若A（1，m）（m>0）为C上一点，O为坐标原点，求C上另一点B的坐标，使得OA⊥OB。

答 案：(I)由题意,该抛物线的焦点到准线的距离为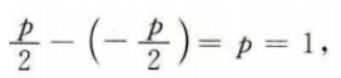 所以抛物线C的方程为y²=2x. (Ⅱ)因A(l,m)(m>0)为C上一点,故有m²=2, 可得 m=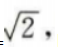因此A点坐标为 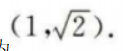设B点坐标为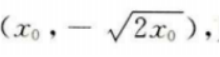

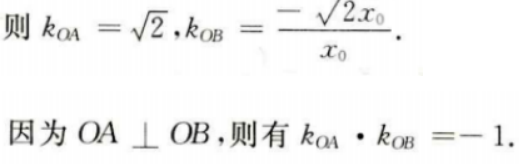
2、已知直线l的斜率为1，l过抛物线C：的焦点，且与C交于A,B两点.
(I）求l与C的准线的交点坐标；
(II）求|AB|．

答 案：(I）C的焦点为，准线为由题意得l的方程为因此l与C的准线的交点坐标为(II）由得设A（x1,y1）.B（x2,y2），则因此

3、如图：已知在△ADC中，∠C=90°，∠D=30°，∠ABC=45°，BD=20，求AC(用小数表示，保留一位小数)  

答 案：如图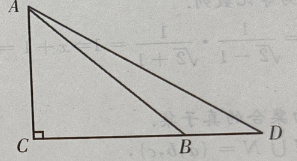  

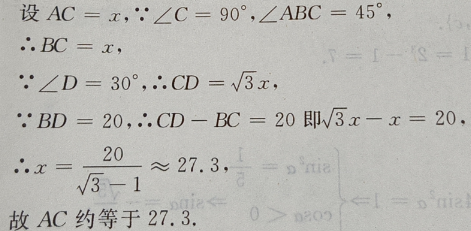
4、设函数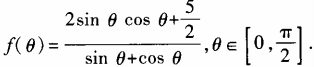 （1）求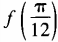；（2）求函数f（θ）最小值。

答 案：

填空题

1、log₂[log₂（log₃81）]=______。  

答 案：1

解 析：由于log₃81=log₃3⁴=4，于是 原式=log₂（log₂4）=log₂2=1。  

2、“x²=4”是“x=2”的______。  

答 案：必要不充分条件