2025年成考高起点每日一练《数学(理)》2月12日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、已知{i，j，k}是单位正交基底，a＝i＋j，b＝－i＋j－k，则a·b＝（）。

• A：-1
• B：1
• C：0
• D：2

答 案：C

解 析：a·b＝（1，1，0）·（－1，1，－1）＝1×（－1）＋1×1＋0×（－1）＝0。答案为C。  

2、若tan(π-α)＞0，且cosα＞0，则α的终边在（）。

• A：第一象限
• B：第二象限
• C：第三象限
• D：第四象限

答 案：D

解 析：∵tan(π-α)＞0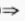-tanα＞0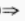tanα＜0,且cosα＞0∴α在第四象限。  

3、函数(x∈R且x≠0)（）。

• A：为奇函数且在(－∞，0)上是减函数
• B：为奇函数且在(－∞，0)上是增函数
• C：为偶函数且在(0，＋∞)上是减函数
• D：为偶函数且在(0，＋∞)上是增函数

答 案：C

解 析：函数 (x∈R且x≠0)为偶函数且在(0,+∞)上是减函数.(答案为C)

4、i为虚数单位，则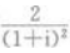的值为（）。

• A：1
• B：－1
• C：i
• D：－i

答 案：D

解 析：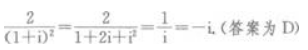

主观题

1、已知tan²θ=2tan²ψ+1，求cos2θ+sin²ψ的值。

答 案：由已知，得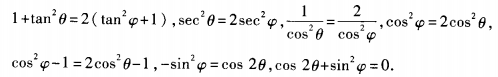

2、求（1+tan10°）（1+tan35°）的值。  

答 案：原式=1+tan10°+tan35°+tan10°·tan35°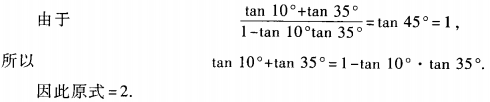

3、已知lg2=a，lg3=b，求lg0.15关于a，b的表达式。  

答 案：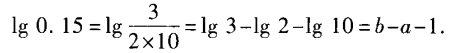

4、（1）已知tanα=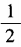，求cot2α的值； （2）已知tan2α=1，求tanα的值。

答 案：（1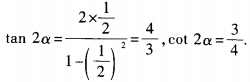）（2）由已知，得 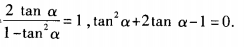解关于tanα的一元二次方程，得tanα=  

填空题

1、lg(tan43°tan45°tan47°)=（）  

答 案：0

解 析：lg(tan43°tan45°tan47°)=lg(tan43°tan45°cot43°)=lgtan45°=lg1=0

2、sin²10°+sin²20°+sin²40°+sin²50°+sin²70°+sin²80=______。

答 案：3

解 析：由互为余角的余函数值相等得 原式=(sin²10°+cos²10°)+(sin²20°+cos²20°)+(sin²40+cos²40)=1+1+1=3