2025年成考高起点每日一练《数学(文史)》2月7日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、函数（）。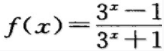

• A：是偶函数
• B：是奇函数
• C：既是奇函数，又是偶函数
• D：既不是奇函数，又不是偶函数

答 案：B

2、盒中有20节电池，其中有2节是废品，现从中取3节，其中至少有一节废品的概率是（）。

• A：
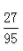
• B：
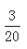
• C：
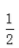
• D：

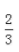
答 案：A

3、y=(2x²+3)(3x-2)的导数是（　）

• A：18x²-8x+9
• B：6x²+9
• C：12x²-8x
• D：12x

答 案：A

解 析：y=(2x²+3)(3x-2)=6x³-4x2+9x-6，y´=18x²-8x+9．【考点指要】会用两个函数和、差的求导法则求多项式函数的导数，是近几年成人高考的常见题．

4、甲、乙两个人各进行一次射击，甲击中目标的概率是0.2，乙击中目标的概率是0.7，则甲、乙两人都击中目标的概率是（）。

答 案：A

解 析：本题属于相互独立事件同时发生的概率，设A为甲击中目标的事件，B为乙击中目标的事件，P（A）=O.2，P（B）=0.7，P（A·B）=P（A）·P（B）=O.2×0.7=0.14，故应选A。

主观题

1、设函数f(x)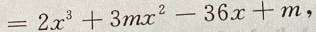且f'(-1)=-36 (Ⅰ)求m (Ⅱ)求f(x)的单调区间

答 案：(Ⅰ)由已知得f'=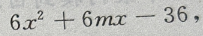 又由f'(-1)=-36得 6-6m-36=-36 故m=1. (Ⅱ)由(Ⅰ)得f'(x)=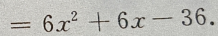 令f'(x)=0，解得 当x<-3时，f'(x)>0; 当-32时，f'(x)>0; 故f(x)的单调递减区间为(-3,2)，f(x)的单调递增区间为(-∞,-3),(2,+∞)  

2、设全集U=R，集合A={x｜-5＜x＜5}，B={x｜0≤x≤7}，求CUA∩B．

答 案：解：全集U=R，A={x｜-5＜x＜5}，B=｛X｜0≤x≤7}，因为CuA={x｜x≤-5或x≥5}，所以CuA∩B={x｜x≤-5或x≥5}N{x｜0≤x≤7}={x｜5≤x≤7}，如图1—10所示。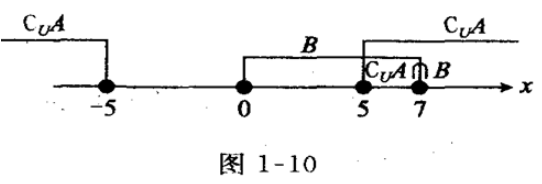

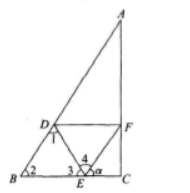
3、在△ABC中，已知AB=2,BC=1,CA=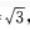 点D,E,F分别在AB,BC,CA边上，△DEF为正三角形，记∠FEC为α，如果sinα= 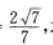求△DEF的边长。

答 案：解析:由AB=2，BC=1,CA=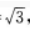 得BC²=CA²=AB²,因此∠C=90°，如图所示。 因为sinA= 所以∠A=30°，于是∠b=60°。 设正△DEF边长为l，已知AB=2,sinα=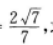 由此EC=lcosα 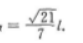有图知，∠1+∠2+∠3=180°（三角形内角和）； ∠3+∠4+α=180°，因为∠2-∠4=60°，所以∠1=α。 【考点指要】本题主要考查三角函数的概念、同角三角函数的关系及正弦定理，这些均是考试大纲要求掌握的重要概念，并要求能达到灵活应用的程度，此类题是在成人高考中出现频率较高的题型，

4、如图：已知在△ADC中，∠C=90°，∠D=30°，∠ABC=45°，BD=20，求AC(用小数表示，保留一位小数)  

答 案：如图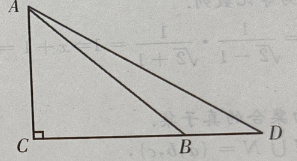  

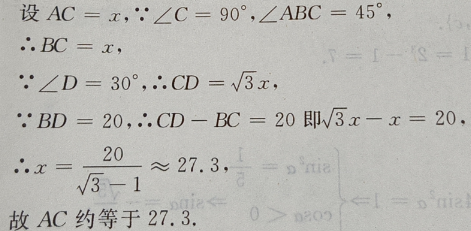
填空题

1、在1000000张奖券中，设有1个一等奖，5个二等奖，10个三等奖，从中买一张奖券，中奖的概率是______。  

答 案：

解 析：本题试验属于等可能事件的概率。n=1000000，m=16，所以买一张奖券，中奖的概率

2、函数y=-x²+ax图像的对称轴为x=2，则a=______。

答 案：4  

解 析：本题主要考查的知识点为二次函数的性质。 由题意，该函数图像的对称轴为得a=4。