2025年成考高起点每日一练《数学(理)》2月4日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、袋中有6个球,其中4个红球,2个白球,从中随机取出2个球,则其中恰有1个红球的概率为()
- A:

- B:
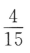
- C:

- D:
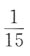
答 案:A
解 析: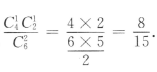
2、若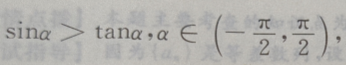 则
则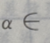 ()
()
- A:

- B:

- C:
- D:
答 案:B
解 析:首先做出单位圆,然后根据问题的约束条件,利用三角函数线找出满足条件的a角取值范围 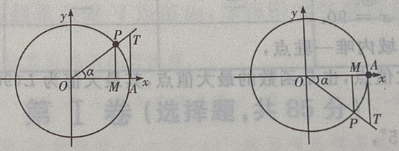
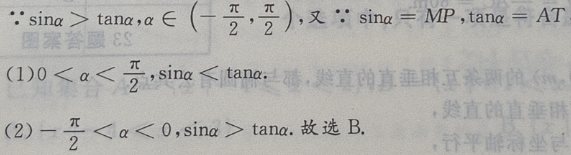
3、函数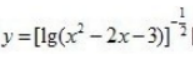 定义域为()。
定义域为()。
- A:{x|x<3,x∈R}
- B:{x|x>-1.x∈R}
- C:{x|-1<x<3,x∈R}
- D:{x|<-1或x>3,x∈R}
答 案:D
4、过点(-2,2)与直线x+3y-5=0平行的直线是()
- A:x+3y-4=0
- B:3x+y+4=0
- C:x+3y+8=0
- D:3x-y+8=0
答 案:A
解 析:所求直线与x+3y-5=0平行,可设所求直线为x+3y+c=0,将点(一2,2)带入直线方程,故-2+3×2+c=0,解得c=-4,因此所求直线为线为x+3y-4=0.
主观题
1、设 (0<α<π),求tanα的值。
(0<α<π),求tanα的值。
答 案:
2、设A1A2A3A4A5A6为正六边形,如图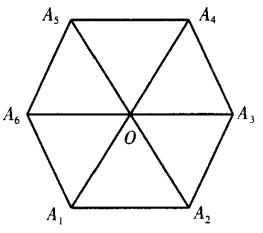 ,O为它的中心。 (1)求证:
,O为它的中心。 (1)求证: 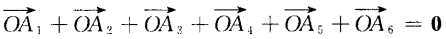 (2)
(2)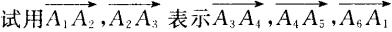
答 案:已知A1A2A3A4A5A6 为正六边形,即|A1A2|=|A3A4|=......|A6A1|.要证6个向量的和为0.只需证其中3个向量与另3个向量的长度相等、方向相反即可.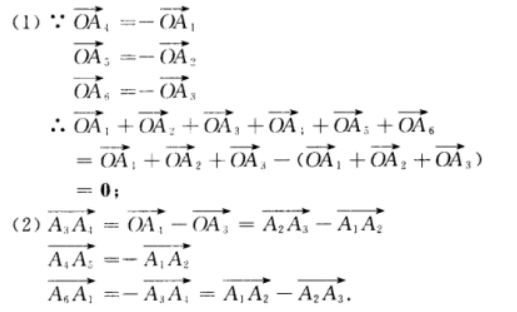
3、在△ABC中如果sinA=2sinBcosC,求证:△ABC是等腰三角形。
答 案: ∴△ABC为等腰三角形。
∴△ABC为等腰三角形。
4、求下列函数的最大值、最小值和最小正周期: (1)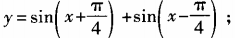 (2)y=6cosx+8sinx
(2)y=6cosx+8sinx
答 案:
填空题
1、sin210°+sin220°+sin240°+sin250°+sin270°+sin280=______。
答 案:3
解 析:由互为余角的余函数值相等得 原式=(sin210°+cos210°)+(sin220°+cos220°)+(sin240+cos240)=1+1+1=3
2、已知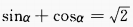 ,则
,则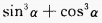 =______。
=______。
答 案:
解 析:

精彩评论